题目内容
5．已知点A的坐标为（3，1），F是抛物线y2=4x的焦点，P是抛物线上的动点，求|PA|+|PF|的最小值．分析 设点P在准线上的射影为D，则根据抛物线的定义可知|PF|=|PD|进而把问题转化为求|PA|+|PD|取得最小，进而可推断出当D，P，A三点共线时|PA|+|PD|最小，答案可得．
解答 解：设点P在准线上的射影为D，则根据抛物线的定义可知|PF|=|PD|，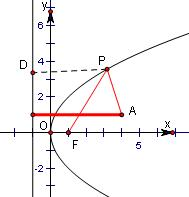
∴要求|PA|+|PF|取得最小值，即求|PA|+|PD|取得最小
当D，P，A三点共线时|PA|+|PD|最小，
由A点坐标为（3，1），抛物线y2=4x的准线方程为x=-1，
故此时|PA|+|PD|=|AD|=3-（-1）=4．
即|PA|+|PF|的最小值为4．
点评 本题考查抛物线的定义、标准方程，以及简单性质的应用，判断当D，P，A三点共线时|PA|+|PD|最小，是解题的关键．
练习册系列答案
中考解读考点精练系列答案
各地期末复习特训卷系列答案
相关题目
13．Sn=1+（1+$\frac{1}{2}$）+（1+$\frac{1}{2}$+$\frac{1}{4}$）+…（1+$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n-1}}$）等于（ ）
| A． | $\frac{1}{{2}^{n}}$ | B． | 2n+$\frac{1}{{2}^{n-1}}$ | C． | 2n-2+$\frac{1}{{2}^{n-1}}$ | D． | $\frac{n-1}{{2}^{n-1}}$ |
20．如果抛物线f（x）=x2+bx+c与x轴交于两点（-1，0）和（3，0），则f（x）＞0的解是（ ）
| A． | （-1，3） | B． | [-1，3] | C． | （-∞，-1）∪（3，+∞） | D． | （-∞，-1]∪[3，+∞） |