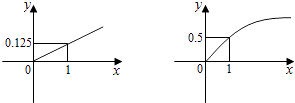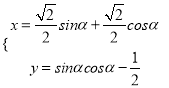题目内容
【题目】设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x﹣2)=f(x+2)且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
【答案】( ![]() ,2)
,2)
【解析】解:∵对于任意的x∈R,都有f(x﹣2)=f(2+x),∴函数f(x)是一个周期函数,且T=4.
又∵当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,且函数f(x)是定义在R上的偶函数,
)x﹣1,且函数f(x)是定义在R上的偶函数,
若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0恰有3个不同的实数解,
则函数y=f(x)与y=loga(x+2)在区间(﹣2,6]上有三个不同的交点,如下图所示: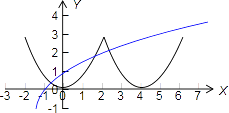
又f(﹣2)=f(2)=3,
则对于函数y=loga(x+2),由题意可得,当x=2时的函数值小于3,当x=6时的函数值大于3,
即loga4<3,且loga8>3,由此解得: ![]() <a<2,
<a<2,
所以答案是:( ![]() ,2).
,2).

练习册系列答案
相关题目
【题目】某车间生产某种产品,固定成本是![]() 万元,每生产
万元,每生产![]() 件产品成本增加
件产品成本增加![]() 元,根据经验,当年产量少于400件时,总收益
元,根据经验,当年产量少于400件时,总收益![]() (成本与总利润的和,单位:元)是年产量
(成本与总利润的和,单位:元)是年产量![]() (单位:件)的二次函数;,当年产量不少于
(单位:件)的二次函数;,当年产量不少于![]() 件时,R是Q的一次函数,以下是Q与R的部分数据:
件时,R是Q的一次函数,以下是Q与R的部分数据:
Q/ 件 | 50 | 200 | 350 | 500 | 650 |
R/ 元 | 23750 | 80000 | 113750 | 125000 | 1332500 |
问:每年生产多少件产品时,总利润最大?最大利润为多少?