题目内容
17.在△ABC中,a、b、c分别是∠A、∠B、∠C的对应边长,已知2sin2A=3cosA.(1)求∠A;
(2)若a=$\sqrt{3}$,求△ABC面积的最大值.
分析 (1)根据已知等式求得cosA的值,进而求得A.
(2)根据余弦定理建立等式,利用基本不等式的性质确定bc的最大值,进而代入三角形面积公式求得面积的最大值.
解答 解:(1)∵2sin2A=3cosA,
∴2(1-cos2A)=3cosA,
∴2cos2A+3cosA-2=0,
解得cosA=$\frac{1}{2}$,
∵0<A<π,
∴A=$\frac{π}{3}$.
(2)∵S△ABC=$\frac{1}{2}$bcsinA=$\frac{\sqrt{3}}{4}$bc,
又∵b2+c2-a2=bc,
∴a2=b2+c2-bc≥2bc-bc=bc,
当且仅当a=b时等号成立,
∴bc≤a2=($\sqrt{3}$)2=3,
∴S△ABC≤$\frac{3\sqrt{3}}{4}$.即△ABC面积的最大值是$\frac{3\sqrt{3}}{4}$.
点评 本题主要考查了正弦定理和余弦定理的运用.解题的关键是确定bc的范围.

练习册系列答案
相关题目
7.过原点的直线与圆x2+y2-6x+5=0相交于A,B两点,则弦AB的中点M的轨迹方程为( )
| A. | x2+y2+3x=0 | B. | x2-y2-3x=0 | C. | x2-y2+3x=0 | D. | x2+y2-3x=0 |
8.若抛物线y=ax2在点x=1处的切线与直线x+2y=0垂直,则a=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
5.函数f(x)=x3+bx2+cx+d的图象如图所示,则函数g(x)=log2(x2+$\frac{2b}{3}$+$\frac{c}{3}$)的单调递减区间是( )
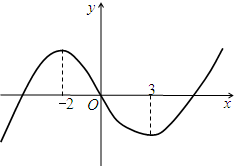

| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
12.数列{an}的各项都是正数,且数列{log3an}是等差数列,若a5a6+a4a7=18,则log3a1+log3a2+…+log3a10=( )
| A. | 12 | B. | 10 | C. | 8 | D. | 2+log35 |
9.下列函数中,是偶函数且图象关于x=$\frac{π}{2}$对称的函数是( )
| A. | y=sin2x | B. | y=cosx | C. | y=sin($\frac{π}{2}$-2x) | D. | y=tanx |
6.8名学生和2位老师站成一排合影,2位老师恰好相邻的排法种数为( )
| A. | A${\;}_{9}^{9}$A${\;}_{2}^{2}$ | B. | A${\;}_{9}^{9}$ | C. | A${\;}_{10}^{10}$ | D. | 2A${\;}_{10}^{9}$ |