题目内容
已知命题p:“?x∈[0,2],x2-a≥0”,命题q:“?x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是______.
因为:“?x∈[0,2],x2-a≥0”,所以a≤x2,所以a≤0,即p:a≤0.
若:“?x∈R,x2+2ax+2-a=0,则△≥0,即4a2-4(2-a)≥0,
所以a2+a-2≥0,解得a≥1或a≤-2.
即q:a≥1或a≤-2.
若命题“p且q”是真命题,则p,q同时为真命题.
所以a≤-2.
故答案为:{a|a≤-2}.
若:“?x∈R,x2+2ax+2-a=0,则△≥0,即4a2-4(2-a)≥0,
所以a2+a-2≥0,解得a≥1或a≤-2.
即q:a≥1或a≤-2.
若命题“p且q”是真命题,则p,q同时为真命题.
所以a≤-2.
故答案为:{a|a≤-2}.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
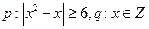 且“
且“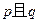 ”与“非
”与“非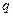 ”同时为假命题,求
”同时为假命题,求 的值。
的值。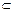 平面β,有下列四个命题:①
平面β,有下列四个命题:①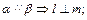
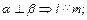 ③
③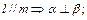 ④
④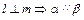 。其中真命题是
。其中真命题是