题目内容
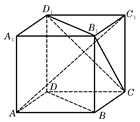
如图,在四棱锥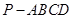 中,
中,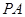 ⊥底面
⊥底面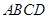 ,底面
,底面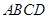 为梯形,
为梯形,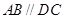 ,
,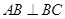 ,
,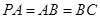 ,点
,点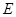 在棱
在棱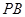 上,且
上,且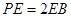 .
.
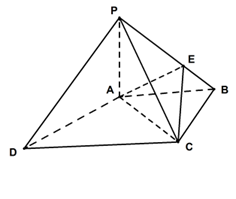
(1)求证:平面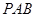 ⊥平面
⊥平面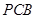 ;
;
(2)求平面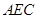 和平面
和平面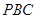 所成锐二面角的余弦值.
所成锐二面角的余弦值.
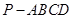 中,
中,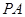 ⊥底面
⊥底面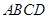 ,底面
,底面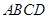 为梯形,
为梯形,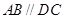 ,
,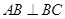 ,
,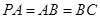 ,点
,点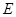 在棱
在棱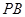 上,且
上,且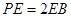 .
.
(1)求证:平面
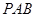 ⊥平面
⊥平面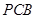 ;
;(2)求平面
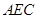 和平面
和平面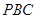 所成锐二面角的余弦值.
所成锐二面角的余弦值.(1)见解析(2)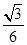
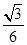
试题分析:(1)证明:∵
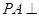 底面
底面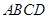 ,∴
,∴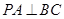 .又
.又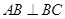 ,
,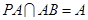 ,
,∴
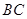 ⊥平面
⊥平面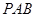 , 又
, 又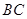
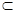 平面
平面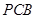 ,∴平面
,∴平面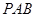 ⊥平面
⊥平面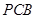 ………………4分
………………4分(2)以
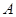 为原点,
为原点,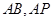 所在直线分别为
所在直线分别为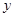 轴、
轴、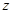 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.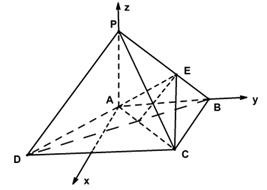
设
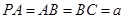 ,则
,则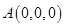 ,
,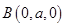 ,
,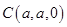 ,
,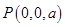 ,
,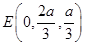 .
.设
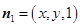 为平面
为平面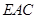 的一个法向量,则
的一个法向量,则 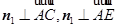 ,∴
,∴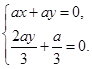 ,
,解得
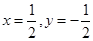 ,∴
,∴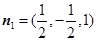 .
.设
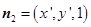 为平面
为平面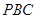 的一个法向量,
的一个法向量,则
 ,又
,又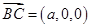 ,
,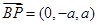 ,
,∴
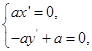 ,解得
,解得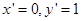 ,
,∴
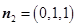 .
. 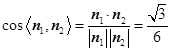 .
. ∴平面
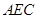 和平面
和平面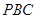 所成锐二面角的余弦值为
所成锐二面角的余弦值为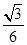 …………………………10分
…………………………10分点评:空间向量引入立体几何使立体几何的思维量减少了很多,在解决立体几何题目时效果明显

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
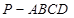 中,
中,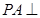 平面
平面 ,
,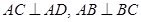 ,
,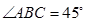 ,
,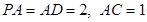 .
.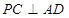 ;
; 的正弦值;
的正弦值;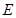 为棱
为棱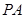 上的点,满足异面直线
上的点,满足异面直线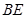 与
与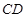 所成的角为
所成的角为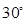 ,求
,求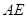 的长.
的长.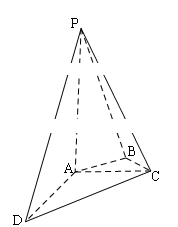

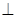 A1D;
A1D;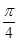 。
。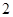 的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=
的正方形,PD⊥平面ABCD,EC∥PD,且PD=2EC=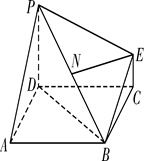
 到平面
到平面 的距离.
的距离.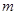 、
、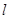 ,两个不同平面
,两个不同平面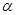 、
、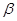 ,给出下列命题:
,给出下列命题: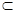
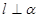 ,则
,则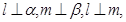 则
则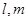 在平面
在平面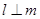 。
。 ,β,γ,给出下列命题:
,β,γ,给出下列命题: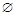 ,则
,则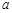 不平行于平面
不平行于平面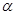 ,则下列结论成立的是( )
,则下列结论成立的是( )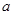 异面
异面