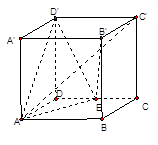
题目内容
(本题满分13分)
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E的棱AB上移动。
(I)证明:D1E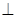 A1D;
A1D;
(II)AE等于何值时,二面角D1-EC-D的大小为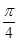 。
。
在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E的棱AB上移动。

(I)证明:D1E
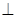 A1D;
A1D;(II)AE等于何值时,二面角D1-EC-D的大小为
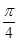 。
。(Ⅰ)见解析;(Ⅱ)二面角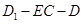 的大小为
的大小为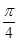 .
.
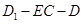 的大小为
的大小为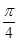 .
.试题分析:(1)欲证DE⊥平面A1E,根据线面垂直的判定定理可知只需证AE⊥DE,A1A⊥DE,即可;
解:以
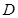 为坐标原点,直线
为坐标原点,直线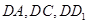 分别为
分别为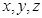 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设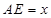 ,则
,则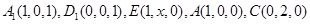 (2分)
(2分)(Ⅰ)
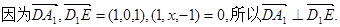 (4分)
(4分)(Ⅱ)设平面
 的法向量
的法向量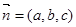 ,
,∴
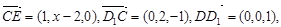
由
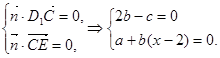 令
令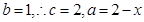 ,
,∴
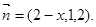 (8分)
(8分)依题意
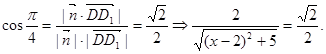
∴
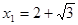 (不合,舍去),
(不合,舍去),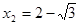 .
.∴
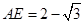 时,二面角
时,二面角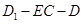 的大小为
的大小为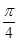 . (13分)
. (13分)点评:解决该试题的关键是能利用向量的知识来表示空间的点,然后借助向量在几何中的运用,求证垂直和二面角的平面角的问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,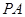 ⊥底面
⊥底面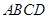 ,底面
,底面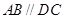 ,
,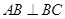 ,
,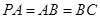 ,点
,点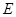 在棱
在棱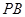 上,且
上,且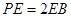 .
.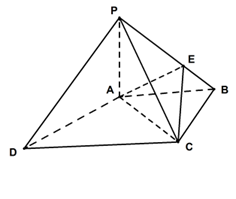
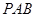 ⊥平面
⊥平面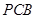 ;
;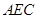 和平面
和平面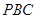 所成锐二面角的余弦值.
所成锐二面角的余弦值. .M为线段PC的中点.
.M为线段PC的中点.

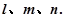 若
若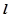 与
与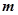 异面,且
异面,且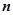 异面,则( )
异面,则( )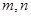 是不同的直线,
是不同的直线,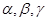 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题: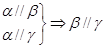 ②
②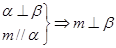 ③
③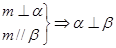 ④
④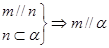
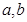 和平面
和平面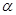 ,且
,且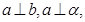 则
则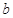 与
与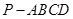 的底面
的底面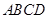 为矩形,且
为矩形,且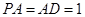 ,
,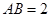 ,
,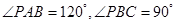 ,(Ⅰ)平面
,(Ⅰ)平面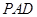 与平面
与平面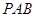 是否垂直?并说明理由;(Ⅱ)求直线
是否垂直?并说明理由;(Ⅱ)求直线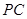 与平面
与平面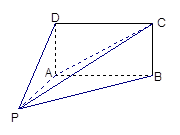
 中,点
中,点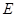 是
是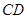 的中点.
的中点. 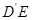 与
与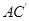 所成的角的余弦值;
所成的角的余弦值;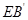 与平面
与平面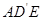 所成的角的余弦值.
所成的角的余弦值.