题目内容
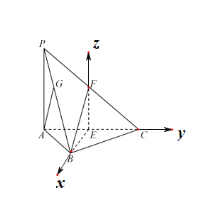
【题目】如图,三棱锥![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
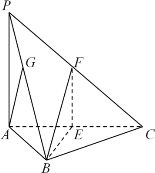
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在;![]() 是
是![]() 的中点
的中点
【解析】
(1)由![]() 底面
底面![]() ,可得
,可得![]() ,再由
,再由![]() ,利用线面垂直的判定定理得到
,利用线面垂直的判定定理得到![]() 平面
平面![]() ,根据
,根据![]() 平面
平面![]() ,由面面垂直的判定定理证明即可.
,由面面垂直的判定定理证明即可.
(2)由![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的正方向为
的正方向为![]() 轴,建立空间直角坐标系,求得平面
轴,建立空间直角坐标系,求得平面![]() 的一个法向量
的一个法向量![]() ,设
,设![]() ,表示
,表示![]() 的坐标,根据直线
的坐标,根据直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() ,由
,由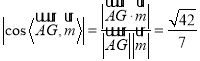 求解.
求解.
(1)因为![]() 底面
底面![]() ,
,![]() 底面
底面![]() ,
,
所以![]() ,
,
易知![]() ,
,![]()
所以![]() 平面
平面![]() ,..
,..
因为![]() 平面
平面![]() ,
,
所以平面![]()
![]() 平面
平面![]()
(2)因为![]() 两两垂直,所以以
两两垂直,所以以![]() 为坐标原点,分别以
为坐标原点,分别以![]() 的正方向为
的正方向为![]() 轴,建立如图所示空间直角坐标系,
轴,建立如图所示空间直角坐标系,
则![]() ,
,
![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由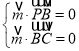 ,得
,得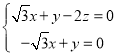 ,
,
不妨设![]() ,则
,则![]() ,所以
,所以![]() ,
,
设![]() ,则
,则![]() ,
,
由题知: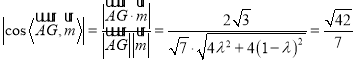 ,
,
即![]() ,
,
解得![]() ,
,
所以在线段![]() 上存在点
上存在点![]() 为PB的中点,使得直线
为PB的中点,使得直线![]() 与平面
与平面![]() 所成的角的余弦值为
所成的角的余弦值为![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某公司准备将1000万元资金投人到市环保工程建设中,现有甲,乙两个建设项目选择,若投资甲项目一年后可获得的利润![]() (万元)的概率分布列如表所示:
(万元)的概率分布列如表所示:
| 110 | 120 | 170 |
|
| 0.4 |
|
且![]() 的期望
的期望![]() ;若投资乙项目一年后可获得的利润
;若投资乙项目一年后可获得的利润![]() (万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为
(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为![]() 和
和![]() .若乙项目产品价格一年内调整次数
.若乙项目产品价格一年内调整次数![]() (次数)与
(次数)与![]() 的关系如表所示:
的关系如表所示:
| 0 | 1 | 2 |
| 41.2 | 117.6 | 204.0 |
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的分布列.
的分布列.
【题目】为助力湖北新冠疫情后的经济复苏,某电商平台为某工厂的产品开设直播带货专场.为了对该产品进行合理定价,用不同的单价在平台试销,得到如下数据:
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)根据以上数据,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若该产品成本是4元/件,假设该产品全部卖出,预测把单价定为多少时,工厂获得最大利润?
(参考公式:回归方程![]() ,其中
,其中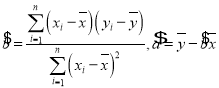 )
)