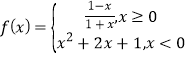题目内容
【题目】已知双曲线
的左、右焦点分别为F1、F2，过点F1作圆x2+y2＝a2的切线交双曲线右支于点M，若tan∠F1MF2＝2，又e为双曲线的离心率，则e2的值为（ ）
A.
B.
C.
D.
【答案】C
【解析】
运用双曲线的定义可得|MF1|﹣|MF2|＝2a，设|MF2|＝t，则|MF1|＝2a+t，sin∠MF1F2
，然后在三角形MF1F2中由正、余弦定理列方程可解得离心率的平方.
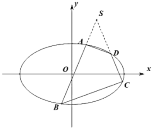
如图：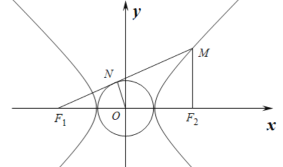
|MF1|﹣|MF2|＝2a，设|MF2|＝t，则|MF1|＝2a+t，
∵sin∠MF1F2，
若tan∠F1MF2＝2，则sin∠F1MF2
，cos∠F1MF2
，
在△MF1F2中，由正弦定理得
，即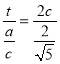
，
∴t
a，∴|MF2|a，|MF1|＝（
2）a，
由余弦定理得4c2＝5a2+（9+4
）a2﹣2
a×（2
）a
，
4c2＝（10+2）a2，∴c2═
a2，∴e2
.
故选：C.
练习册系列答案
相关题目
