题目内容
【题目】（1）写出下列两组诱导公式：
①关于
与
的诱导公式；
②关于
与的诱导公式.
（2）从上述①②两组诱导公式中任选一组，用任意角的三角函数定义给出证明.
【答案】（1）详见解析（2）详见解析
【解析】
（1）按要求写出对应公式即可.（2）利用任意角定义以及对称性即可证明对应公式.
解：（1）①
，
，
.
②
，
，
.
（2）①证明：设任意角
的终边与单位圆的交点坐标为
.
由于角
的终边与角的终边关于
轴对称，
因此角的终边与单位圆的交点
与点
关于轴对称，
所以点的坐标是
.
由任意角的三角函数定义得，
，
，
；
，
，
.
所以，，..
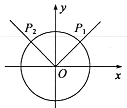
②证明：设任意角的终边与单位圆的交点坐标为.
由于
角的终边与角的终边关于
轴对称，
因此角的终边与单位圆的交点与点关于轴对称，
所以点的坐标是
.
由任意角的三角函数定义得，
，，；
，
，
.
所以，，.
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
【题目】为了解学生的课外阅读时间情况，某学校随机抽取了50人进行统计分析，把这50人每天阅读的时间（单位：分钟）绘制成频数分布表，如下表所示：
阅读时间 | [0,20） | [20,40） | [40,60） | [60,80） | [80,100） | [100,120] |
人数 | 8 | 10 | 12 | 11 | 7 | 2 |
若把每天阅读时间在60分钟以上（含60分钟）的同学称为“阅读达人”，根据统计结果中男女生阅读达人的数据，制作出如图所示的等高条形图：
（1）根据已知条件完成2x2列联表;
男生 | 女生 | 总计 | |
阅读达人 | |||
非阅读达人 | |||
总计 |
（2）并判断是否有
的把握认为“阅读达人”跟性别有关？
附：参考公式
