题目内容
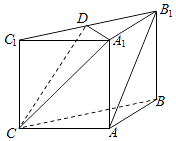
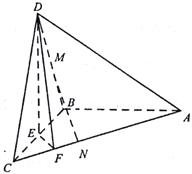
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() .
.![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点,求证:
的中点,求证:

(Ⅰ)![]() 底面
底面![]() ;
;
(Ⅱ)![]() 平面
平面![]() ;
;
(Ⅲ)平面![]() 平面
平面![]() .
.
【答案】把平面与平面垂直转化为直线和平面垂直是常见的转化.要证直线和平面垂直,依据相关判定定理转化为证明直线和直线垂直.要证直线和平面平行,可以利用直线和平面平行的判定定理完成。证明平面与平面垂直,需要在一个平面内找到一条和另一个平面垂直的直线,依据平面与平面垂直的判定定理。
【解析】(Ⅰ)因为平面![]() 底面
底面![]() ,且
,且![]() 垂直于这两个平面的交线
垂直于这两个平面的交线![]() ,
,
所以![]() 底面
底面![]() .
.
(Ⅱ)因为![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]() ,且
,且![]() .
.
所以![]() 为平行四边形.
为平行四边形.
所以![]() ,.
,.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅲ)因为![]() ,并且
,并且![]() 为平行四边形,
为平行四边形,
所以![]() ,
,![]() .
.
由(Ⅰ)知![]() 底面
底面![]() ,
,
所以![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]() .
.
因为![]() 和
和![]() 分别是
分别是![]() 和
和![]() 的中点,
的中点,
所以![]() .
.
所以![]() .
.
所以![]() 平面
平面![]() .
.
所以平面![]() 平面
平面![]() .
.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: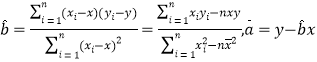 .
.