题目内容
设V为全体平面向量构成的集合,若映射f:
V→R满足:
对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f[λa+(1-λ)b]=λf(a)+(1-λ)f(b),则称映射f具有性质p.
现给出如下映射:
①f1:V→R,f1(m)=x-y,m=(x,y)∈V;
②f2:V→R,f2(m)=x2+y,m=(x,y)∈V;
③f3:V→R,f3(m)=x+y+1,m=(x,y)∈V.
分析映射①②③是否具有性质p.
V→R满足:
对任意向量a=(x1,y1)∈V,b=(x2,y2)∈V,以及任意λ∈R,均有f[λa+(1-λ)b]=λf(a)+(1-λ)f(b),则称映射f具有性质p.
现给出如下映射:
①f1:V→R,f1(m)=x-y,m=(x,y)∈V;
②f2:V→R,f2(m)=x2+y,m=(x,y)∈V;
③f3:V→R,f3(m)=x+y+1,m=(x,y)∈V.
分析映射①②③是否具有性质p.
①具有性质p②不具有性质p. ③具有性质p.
a=(x1y1),b=(x2,y2),
λa+(1-λ)b=(λx1+(1-λ)x2,λy1+(1-λ)y2).
对于①,f1(m)=x-y
∴f(λa+(1-λ)b)=[λx1+(1-λ)x2]-[λy1+(1-λ)y2]
=λ(x1-y1)+(1-λ)(x2-y2).
λf(a)+(1-λ)f(b)=λ(x1-y1)+(1-λ)(x2-y2)
f(λa+(1-λ)b)=λf(a)+(1-λ)f(b).
∴①具有性质p.
对于②,f2(m)=x2+y,设a=(0,0),b=(1,2),
λa+(1-λ)b=(1-λ,2(1-λ)),
f(λa+(1-λ)b)=(1-λ)2+2(1-λ)=λ2-4λ+3,
而λf(a)+(1-λ)b=λ(02+0)+(1-λ)(12+2)=3(1-λ).
又λ∈R,∴f(λa+(1-λ)b)=λf(a)+(1-λ)f(b)不恒成立
故②不具有性质p.
对于③,f3(m)=x+y+1,
f(λa+(1-λ)b)=[λx1+(1-λ)x2]+[λy1+(1-λ)y2]+1
=λ(x1+y1)+(1-λ)(x2+y2)+1,
又λf(a)+(1-λ)f(b)=λ(x1+y1+1)+(1-λ)(x2+y2+1)
=λ(x1+y1)+(1-λ)(x2+y2)+λ+(1-λ)
=λ(x1+y1)+(1-λ)(x2+y2)+1.
∴f(λa+(1-λ)b)=λf(a)+(1-λ)f(b)
③具有性质p.
λa+(1-λ)b=(λx1+(1-λ)x2,λy1+(1-λ)y2).
对于①,f1(m)=x-y
∴f(λa+(1-λ)b)=[λx1+(1-λ)x2]-[λy1+(1-λ)y2]
=λ(x1-y1)+(1-λ)(x2-y2).
λf(a)+(1-λ)f(b)=λ(x1-y1)+(1-λ)(x2-y2)
f(λa+(1-λ)b)=λf(a)+(1-λ)f(b).
∴①具有性质p.
对于②,f2(m)=x2+y,设a=(0,0),b=(1,2),
λa+(1-λ)b=(1-λ,2(1-λ)),
f(λa+(1-λ)b)=(1-λ)2+2(1-λ)=λ2-4λ+3,
而λf(a)+(1-λ)b=λ(02+0)+(1-λ)(12+2)=3(1-λ).
又λ∈R,∴f(λa+(1-λ)b)=λf(a)+(1-λ)f(b)不恒成立
故②不具有性质p.
对于③,f3(m)=x+y+1,
f(λa+(1-λ)b)=[λx1+(1-λ)x2]+[λy1+(1-λ)y2]+1
=λ(x1+y1)+(1-λ)(x2+y2)+1,
又λf(a)+(1-λ)f(b)=λ(x1+y1+1)+(1-λ)(x2+y2+1)
=λ(x1+y1)+(1-λ)(x2+y2)+λ+(1-λ)
=λ(x1+y1)+(1-λ)(x2+y2)+1.
∴f(λa+(1-λ)b)=λf(a)+(1-λ)f(b)
③具有性质p.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
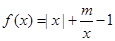
 .
. 时,判断
时,判断 在
在 的单调性,并用定义证明.
的单调性,并用定义证明. ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围;
的取值范围; 上的偶函数
上的偶函数 满足
满足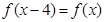 ,且在区间[0,2]上
,且在区间[0,2]上 .若关于
.若关于 的方程
的方程 有三个不同的根,则
有三个不同的根,则 的范围为 .
的范围为 . ,则n的取值集合是________.
,则n的取值集合是________.
 ;
; ,g(x)=
,g(x)= ;
;
 g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )
g(x)是二次函数.若f[g(x)]的值域是[0,+∞),则g(x)的值域是( )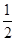
 或-
或-