题目内容
已知定义在 上的偶函数
上的偶函数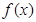 满足
满足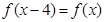 ,且在区间[0,2]上
,且在区间[0,2]上 .若关于
.若关于 的方程
的方程 有三个不同的根,则
有三个不同的根,则 的范围为 .
的范围为 .
 上的偶函数
上的偶函数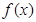 满足
满足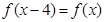 ,且在区间[0,2]上
,且在区间[0,2]上 .若关于
.若关于 的方程
的方程 有三个不同的根,则
有三个不同的根,则 的范围为 .
的范围为 .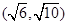
试题分析:因为
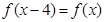 所以此函数为周期函数,且周期为4。因为在区间[0,2]上
所以此函数为周期函数,且周期为4。因为在区间[0,2]上 ,且函数
,且函数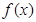 为定义在
为定义在 上的偶函数,则在区间
上的偶函数,则在区间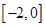 上
上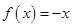 。
。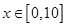 时函数图像如图所示
时函数图像如图所示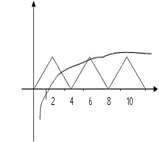
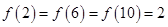 。要使方程
。要使方程 有三个不同的根则有
有三个不同的根则有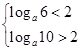 解得
解得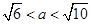 。
。
练习册系列答案
相关题目
 ,
, .
. ;
;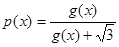 ,求证:
,求证: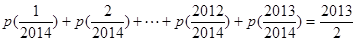 ;
; 是实数集
是实数集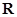 上的奇函数,且
上的奇函数,且 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数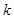 的取值范围.
的取值范围.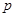 :函数
:函数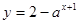 的图象恒过定点
的图象恒过定点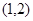 ;命题
;命题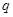 :若函数
:若函数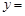
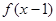 为偶函数,则函数
为偶函数,则函数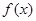 的图象关于直线
的图象关于直线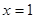 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )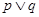
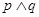
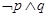
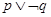
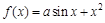 ,若
,若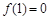 ,则
,则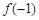 的值为 .
的值为 . B.
B.  C.
C.  D.
D. 
 ]
] D,使得f(x)在[
D,使得f(x)在[ )
) )
) %,第二次提价
%,第二次提价