题目内容
14．已知三点坐标分别为：A（-1，-1），B（1，3），C（2，x），且满足三点共线，则x=（ ）| A． | 5 | B． | -5 | C． | 4 | D． | -4 |
分析 根据A、B、C三点共线，斜率kAB、kAC相等，列出方程，求出x的值．
解答 解：∵A（-1，-1），B（1，3），C（2，x）三点共线，
∴kAB=kAC，
即$\frac{3+1}{1+1}$=$\frac{x+1}{2+1}$，
解得x=5．
故选：A．
点评 本题考查了利用斜率相等解答三点共线的应用问题，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
2．函数f（x）=$\sqrt{2}$sin（ωx+φ）（x∈R，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，则f（0）的值是（ ）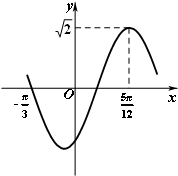
| A． | -$\frac{\sqrt{6}}{2}$ | B． | -$\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{6}}{2}$ |
9．设x，y满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x+y-5≥0}\\{2x-y-3≤0}\end{array}\right.$，若使函数Z=ax+by（2b＞a＞0）的最大值为10，求ab的最大值（ ）
| A． | $\frac{25}{7}$ | B． | $\frac{5}{7}$ | C． | 5 | D． | 25 |
6．点（0，2）关于直线x+2y-1=0的对称点是（ ）
| A． | （-2，0） | B． | （-1，0） | C． | $（-\frac{6}{5}，-\frac{2}{5}）$ | D． | （0，-1） |