题目内容
12.已知f(x)=$\frac{1}{2}{x}^{2}$-mlnx (m∈R)(1)若函数f(x)在($\frac{1}{2}$,+∞)上单调递增,求实数m的取值范围;
(2)当m=2时,求函数f(x)在[1,e]上的最大,最小值;
(3)求f(x)的单调区间.
分析 (1)若函数f(x)在($\frac{1}{2}$,+∞)上是增函数,?f′(x)≥0在($\frac{1}{2}$,+∞)上恒成立.利用二次函数的单调性即可得出;
(2)利用导数研究函数的单调性极值与最值即可得出;
(3)先求出函数f(x)的导数,通过讨论m的范围,从而求出函数的单调区间.
解答 解:(1)若函数f(x)在($\frac{1}{2}$,+∞)上是增函数,
则f′(x)≥0在($\frac{1}{2}$,+∞)上恒成立.
而f′(x)=x-$\frac{m}{x}$,即m≤x2在($\frac{1}{2}$,+∞)上恒成立,
可得m≤$\frac{1}{4}$.
(2)当m=2时,f′(x)=x-$\frac{2}{x}$=$\frac{{x}^{2}-2}{x}$,
令f′(x)=0得x=±$\sqrt{2}$,
当x∈[1,$\sqrt{2}$)时,f′(x)<0,当x∈($\sqrt{2}$,e)时,f′(x)>0.
故x=$\sqrt{2}$是函数f(x)在[1,e]上唯一的极小值点,
故f(x)min=f($\sqrt{2}$)=1-ln2,
又f(1)=$\frac{1}{2}$,f(e)=$\frac{1}{2}$e2-2=$\frac{{e}^{2}-4}{2}$>$\frac{1}{2}$,
故f(x)max=$\frac{{e}^{2}-4}{2}$;
(3)f′(x)=x-$\frac{m}{x}$,(x>0),
当m≤0时,f′(x)>0对x>0恒成立,
∴f(x)在(0,+∞)单调递增,
当m>0时,令f′(x)=0,解得:x=$\sqrt{m}$,
∴0<x<$\sqrt{m}$时,f′(x)<0,f(x)递减,
x>$\sqrt{m}$时,f′(x)>0,f(x)递增.
点评 本题考查了利用导数研究函数的单调性、极值与最值、二次函数的单调性等基础知识与基本技能方法,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 工作代码 | 紧前工作 | 紧后工作 | 工期/天 |
| A | B、E | --- | 1 |
| B | C | A | 5 |
| C | --- | B、D | 3 |
| D | C | E | 2 |
| E | D | A | 1 |
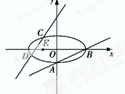 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )| A. | $\frac{7}{6}$ | B. | -$\frac{7}{6}$ | C. | 3 | D. | 6 |

| A. | -$\frac{\sqrt{6}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |

