题目内容
12.某班40个学生平均分成两组,两组学生某次考试的成绩情况如下表所示:| 组别 | 平均数 | 标准差 |
| 第一组 | 90 | 4 |
| 第二组 | 80 | 6 |
标准差$s=\sqrt{\frac{1}{n}[{({x_1}-{{\overline{x)}}^2}+{{({x_2}-\bar\overline{x})}^2}+…+{{({x_n}-\bar\overline{x})}^2}}]}=\sqrt{\frac{1}{n}[{(x_1^2+x_2^2+…+x_n^2)-n{{\bar\overline{x}}^2}}]}$)
分析 根据平均数与方差、标准差的公式,进行计算即可.
解答 解:设第一组同学的分数为ai(1≤i≤20),平均分为$\overline{a}$;
第二组同学的分数为bi(1≤i≤20),平均分为$\overline{b}$;
根据题意得,$\frac{1}{20}$(a1+a2+…+a20)=90,
∴a1+a2+…+a20=1800;
同理,b1+b2+…+b20=1600,
∴全班同学的平均成绩为
$\overline{x}$=$\frac{{(a}_{1}{+a}_{2}+…{+a}_{20})+{(b}_{1}{+b}_{2}+…{+b}_{20})}{20+20}$=85,
又$\sqrt{\frac{1}{20}{{(a}_{1}}^{2}{{+a}_{2}}^{2}+…{{+a}_{20}}^{2}){-\overline{a}}^{2}}$=4,
∴${{a}_{1}}^{2}$+${{a}_{2}}^{2}$+…+${{a}_{20}}^{2}$=162320,
同理${{b}_{1}}^{2}$+${{b}_{2}}^{2}$+…+${{b}_{20}}^{2}$=128720,
∴全班分数的标准差为
s=$\sqrt{\frac{1}{40}{{(a}_{1}}^{2}{{+a}_{2}}^{2}+…{{+a}_{20}}^{2}{{+b}_{1}}^{2}+…{{+b}_{20}}^{2}){-\overline{x}}^{2}}$=$\sqrt{51}$.
点评 本题考查了平均数、方差与标准差的计算问题,是基础题目.

练习册系列答案
相关题目
2.函数f(x)=$\sqrt{2}$sin(ωx+φ)(x∈R,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(0)的值是( )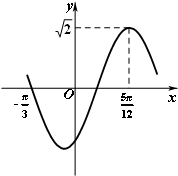

| A. | -$\frac{\sqrt{6}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
7.在单位圆中,面积为2的扇形所对的圆心角为( )弧度.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
1.如图所示程序的输出结果是( )
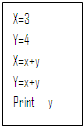
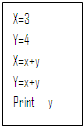
| A. | 4 | B. | 7 | C. | 8 | D. | 11 |