题目内容
如图,在四棱锥P-ABCD中,底面ABCD是梯形,AD∥BC,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.
(Ⅰ)求证:BC⊥平面PAB;
(Ⅱ)求异面直线PC与AB所成角的余弦值;
(Ⅲ)在侧棱PA上是否存在一点E,使得平面CDE与平面ADC所成角的余弦值是
,若存在,求出AE的长;若不存在,说明理由.
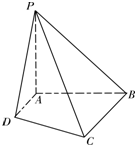
(Ⅰ)求证:BC⊥平面PAB;
(Ⅱ)求异面直线PC与AB所成角的余弦值;
(Ⅲ)在侧棱PA上是否存在一点E,使得平面CDE与平面ADC所成角的余弦值是
| 2 |
| 3 |

(Ⅰ)证明:∵底面ABCD是梯形,AD∥BC,∠DAB=90°,
∴BC⊥AB
∵PA⊥平面ABCD,BC?平面ABCD,∴PA⊥BC,
∵PA∩AB=A,
∴BC⊥平面PAB;
(Ⅱ)以A为原点,分别以AD,AB,AP所在直线x,y,z轴建立空间直角坐标系.
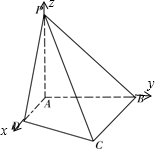
∴A(0,0,0),D(1,0,0),B(0,2,0),C(2,2,0),P(0,0,2).
∴
=(2,2,-2),
=(0,2,0).
∴cos<
,
>=
=
=
∴异面直线PC与AB所成角的余弦值是
…(8分)
(Ⅲ)假设在侧棱PA上存在一点E,使得平面CDE与平面ADC所成角的余弦值是
,
设E(0,0,m)(m>0),∴
=(1,2,0),
=(-1,0,m),
∴设平面CDE的法向量为
=(x,y,z),
∴
•
=0,
•
=0,
∴
令x=2,所以y=-1,z=
,∴
=(2,-1,
).
又∵平面ACD的法向量为
=(0,0,2),
∴cos<
,
>=
=
=
,∴m=1
∴点E的坐标是(0,0,1).
∴在侧棱PA上存在一点E(0,0,1),使得平面CDE与平面ADC所成角的余弦值是
.…(14分)
∴BC⊥AB
∵PA⊥平面ABCD,BC?平面ABCD,∴PA⊥BC,
∵PA∩AB=A,
∴BC⊥平面PAB;
(Ⅱ)以A为原点,分别以AD,AB,AP所在直线x,y,z轴建立空间直角坐标系.

∴A(0,0,0),D(1,0,0),B(0,2,0),C(2,2,0),P(0,0,2).
∴
| PC |
| AB |
∴cos<
| PC |
| AB |
| ||||
|
|
| 4 | ||
4
|
| ||
| 3 |
∴异面直线PC与AB所成角的余弦值是
| ||
| 3 |
(Ⅲ)假设在侧棱PA上存在一点E,使得平面CDE与平面ADC所成角的余弦值是
| 2 |
| 3 |
设E(0,0,m)(m>0),∴
| DC |
| DE |
∴设平面CDE的法向量为
| n |
∴
| n |
| DC |
| n |
| DE |
∴
|
令x=2,所以y=-1,z=
| 2 |
| m |
| n |
| 2 |
| m |
又∵平面ACD的法向量为
| AP |
∴cos<
| n |
| AP |
| ||||
|
|
| ||||
|
| 2 |
| 3 |
∴点E的坐标是(0,0,1).
∴在侧棱PA上存在一点E(0,0,1),使得平面CDE与平面ADC所成角的余弦值是
| 2 |
| 3 |

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
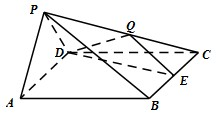
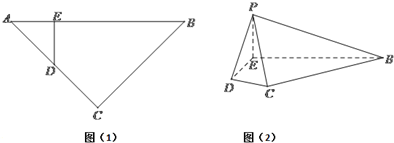

 ,
,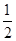 )
)