题目内容
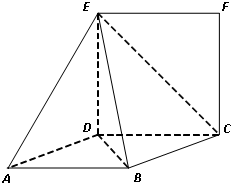
在如图所示的几何体中,四边形ABCD是菱形,ADNM是矩形,平面ADNM⊥平面ABCD,∠DAB=60°,AD=2,AM=1,E为AB的中点.
(Ⅰ)求证:AN∥平面MEC;
(Ⅱ)在线段AM上是否存在点P,使二面角P-EC-D的大小为
?若存在,求出AP的长h;若不存在,请说明理由.

(Ⅰ)求证:AN∥平面MEC;
(Ⅱ)在线段AM上是否存在点P,使二面角P-EC-D的大小为
| π |
| 6 |

(I)CM与BN交于F,连接EF.
由已知可得四边形BCNM是平行四边形,
所以F是BN的中点.
因为E是AB的中点,
所以AN∥EF.…(7分)
又EF?平面MEC,AN?平面MEC,
所以AN∥平面MEC.…(9分)
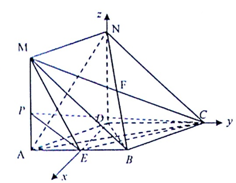 (II)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.
(II)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.
又四边形ADNM是矩形,面ADNM⊥面ABCD,∴DN⊥面ABCD,
如图建立空间直角坐标系D-xyz,则D(0,0,0),E(
,0,0),C(0,2,0),P(
,-1,h),
=(
,-2,0),
=(0,-1,h),设平面PEC的法向量为
=(x,y,z).
则
,∴
,
令y=
h,∴
=(2h,
h,
),又平面ADE的法向量
=(0,0,1),
∴cos<
,
>=
=
=
,解得h=
,
∴在线段AM上是否存在点P,当h=
时使二面角P-EC-D的大小为
.
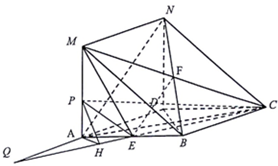
由已知可得四边形BCNM是平行四边形,
所以F是BN的中点.
因为E是AB的中点,
所以AN∥EF.…(7分)
又EF?平面MEC,AN?平面MEC,
所以AN∥平面MEC.…(9分)
 (II)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.
(II)由于四边形ABCD是菱形,E是AB的中点,可得DE⊥AB.又四边形ADNM是矩形,面ADNM⊥面ABCD,∴DN⊥面ABCD,
如图建立空间直角坐标系D-xyz,则D(0,0,0),E(
| 3 |
| 3 |
| CE |
| 3 |
| EP |
| n1 |
则
|
|
令y=
| 3 |
| n1 |
| 3 |
| 3 |
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| ||
|
| ||
| 2 |
| ||
| 7 |
∴在线段AM上是否存在点P,当h=
| ||
| 7 |
| π |
| 6 |


练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目




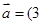 ,
, ,
, ,
, ,且
,且 ∥
∥ ,则
,则 = .
= .