题目内容
【题目】已知函数![]() .
.
(1)若函数![]() 为偶函数,求
为偶函数,求![]() 的值;
的值;
(2)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(3)当![]() 时,若对任意的
时,若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)函数的单调递增区间为
;(2)函数的单调递增区间为![]() ;(3)
;(3)![]() .
.
【解析】
试题(1)由偶函数的定义可得![]() ;(2)将函数写成分段函数的形式,由函数图象可得单调递增区间;(3)由不等式
;(2)将函数写成分段函数的形式,由函数图象可得单调递增区间;(3)由不等式![]() 可得
可得![]() ,再对
,再对![]() 进行分类讨论,目的是去掉绝对值,再根据单调性可得
进行分类讨论,目的是去掉绝对值,再根据单调性可得![]() 的取值范围.
的取值范围.
试题解析:(1)任取![]() ,则有
,则有![]() 恒成立,
恒成立,
即![]() 恒成立
恒成立
![]() 恒成立,
恒成立,![]() 恒成立
恒成立![]()
(2)当![]() 时,
时,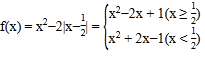
由函数的图像可知,函数的单调递增区间为![]() 。
。
(3)不等式![]() 化为
化为![]()
即:![]() (*)
(*)
对任意的![]() 恒成立
恒成立
因为![]() ,所以分如下情况讨论:
,所以分如下情况讨论:
①![]() 时,不等式(*)化为
时,不等式(*)化为![]() 恒成立
恒成立
即![]()
![]() 上单调递增
上单调递增
只需![]()
![]()
②当![]() 时,不等式(*)化为
时,不等式(*)化为![]() 恒成立
恒成立
即![]()
由①知![]() ,
,![]()
![]()
![]()
![]()
③当![]() 时,不等式(*)化为
时,不等式(*)化为![]() 恒成立
恒成立
即![]()
![]()
![]() 由②得:
由②得:![]()
综上所述,![]() 的取值范围是:
的取值范围是:![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】某种蔬菜从1月1日起开始上市,通过市场调查,得到该蔬菜种植成本![]() (单位:元/
(单位:元/![]() )与上市时间
)与上市时间![]() (单位:10天)的数据如下表:
(单位:10天)的数据如下表:
时间 | 5 | 11 | 25 |
种植成本 | 15 | 10.8 | 15 |
(1)根据上表数据,从下列函数:![]() ,
,![]() ,
,![]() ,
,![]() 中(其中
中(其中![]() ),选取一个合适的函数模型描述该蔬菜种植成本
),选取一个合适的函数模型描述该蔬菜种植成本![]() 与上市时间
与上市时间![]() 的变化关系;
的变化关系;
(2)利用你选取的函数模型,求该蔬菜种植成本最低时的上市时间及最低种植成本.