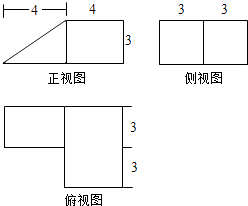
题目内容
【题目】在直角坐标系xOy中,圆C的参数方程![]() (φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆C的极坐标方程;
(Ⅱ)直线l的极坐标方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() , 射线OM:θ=
, 射线OM:θ=![]() 与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O,P,与直线l的交点为Q,求线段PQ的长.
【答案】解:(I)圆C的参数方程![]() (φ为参数).消去参数可得:(x﹣1)2+y2=1.
(φ为参数).消去参数可得:(x﹣1)2+y2=1.
把x=ρcosθ,y=ρsinθ代入化简得:ρ=2cosθ,即为此圆的极坐标方程.
(II)如图所示,由直线l的极坐标方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() ,射线OM:θ=
,射线OM:θ=![]() .
.
可得普通方程:直线ly+![]() x=3
x=3![]() ,射线OMy=
,射线OMy=![]() x.
x.
联立![]() ,解得
,解得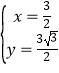 ,即Q
,即Q![]() .
.
联立![]() ,解得
,解得![]() 或
或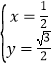 .
.
∴P![]() .
.
∴|PQ|=![]() =2.
=2.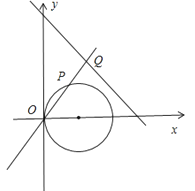
【解析】(I)圆C的参数方程![]() (φ为参数).消去参数可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化简即可得到此圆的极坐标方程.
(φ为参数).消去参数可得:(x﹣1)2+y2=1.把x=ρcosθ,y=ρsinθ代入化简即可得到此圆的极坐标方程.
(II)由直线l的极坐标方程是ρ(sinθ+![]() cosθ)=3
cosθ)=3![]() , 射线OM:θ=
, 射线OM:θ=![]() . 可得普通方程:直线lly+
. 可得普通方程:直线lly+![]() x=3
x=3![]() , 射线OMy=
, 射线OMy=![]() x.分别与圆的方程联立解得交点,再利用两点间的距离公式即可得出.
x.分别与圆的方程联立解得交点,再利用两点间的距离公式即可得出.

【题目】已知函数![]() 的定义域为(0,+
的定义域为(0,+![]() ),若
),若![]() 在(0,+
在(0,+![]() )上为增函数,则称
)上为增函数,则称![]() 为“一阶比增函数”;若
为“一阶比增函数”;若![]() 在(0,+
在(0,+![]() )上为增函数,则称
)上为增函数,则称![]() 为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为
为”二阶比增函数”。我们把所有“一阶比增函数”组成的集合记为![]() 1,所有“二阶比增函数”组成的集合记为
1,所有“二阶比增函数”组成的集合记为![]() 2。
2。
(1)已知函数![]() ,若
,若![]() ∈
∈![]() 1,求实数
1,求实数![]() 的取值范围,并证明你的结论;
的取值范围,并证明你的结论;
(2)已知0<a<b<c,![]() ∈
∈![]() 1且
1且![]() 的部分函数值由下表给出:
的部分函数值由下表给出:
|
|
|
|
|
|
|
| t | 4 |
求证:![]() ;
;
(3)定义集合![]() ,且存在常数k,使得任取x∈(0,+
,且存在常数k,使得任取x∈(0,+![]() ),
),![]() <k},请问:是否存在常数M,使得任意的
<k},请问:是否存在常数M,使得任意的![]() ∈
∈![]() ,任意的x∈(0,+
,任意的x∈(0,+![]() ),有
),有![]() <M成立?若存在,求出M的最小值;若不存在,说明理由。
<M成立?若存在,求出M的最小值;若不存在,说明理由。
【题目】2018年3月山东省高考改革实施方案发布:2020年夏季高考开始全省高考考生总成绩将由语文、数学、外语三门统一高考成绩和学生自主选择的普通高中学业水平等级性考试科目的成绩共同构成.省教育厅为了解正就读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见.右面是根据样本的调查结果绘制的等高条形图.

(Ⅰ)请根据已知条件与等高条形图完成下面的![]() 列联表:
列联表:
赞成 | 不赞成 | 合计 | |
城镇居民 | |||
农村居民 | |||
合计 |
(Ⅱ)试判断我们是否有95%的把握认为“赞成高考改革方案与城乡户口有关”?.
【附】![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 7.879 | 10.828 |