题目内容
5.假设在10秒内的任何时刻,两条不相关的短信机会均等第进入同一部手机,若这两条短信进入手机的时间之差大于3秒,手机就会不受到干扰,则手机不受到干扰的概率为$\frac{49}{100}$.分析 根据几何概型的概率公式求出对应的测度,即可得到结论
解答 解:分别设两个互相独立的短信收到的时间为x,y.则所有事件集可表示为0≤x≤10,0≤y≤10.
由题目得,如果手机受则到干扰的事件发生,必有|x-y|≤3.
则该事件即为x-y=3和y-x=3在0≤x≤10,0≤y≤10的正方形中围起来的图形,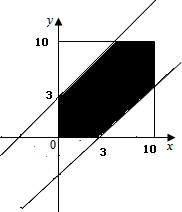
即图中阴影区域,而所有事件的集合即为正方型面积102=100,
阴影部分的面积2×$\frac{1}{2}$(10-3)2=49,
所以阴影区域面积和正方形面积比值即为手机不受到干扰的概率为$\frac{49}{100}$.
故答案为:$\frac{49}{100}$
点评 本题主要考查几何概型的概率的计算,分别求出对应区域的面积是解决本题的关键,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.若函数f(x)=x+$\frac{b}{x}$(b∈R)的导函数在区间(2,4)上有零点,则f(x)在下列区间单调递增的是( )
| A. | (2,+∞) | B. | (-∞,-3) | C. | ($\sqrt{2}$,2) | D. | (-8,-4) |
20.已知a>0且a≠1,函数f(x)=loga(x2-ax+$\frac{1}{2}$)有最小值,则实数a的取值范围是( )
| A. | (0,1) | B. | (0,1)∪(1,$\sqrt{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
10.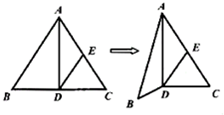 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
 如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )
如图,已知DE是正△ABC的中位线,沿AD将△ABC折成直二面角B-AD-C,则翻折后异面直线AB与DE所成角的余弦值为( )| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | 0 |
15.已知一个正方体的各顶点都在同一个球面上,现用一个平面去截这个球和正方体,得到的截面图形刚好是一个圆及内接正三角形.若此正三角形的边长为a,则这个球的表面积为 ( )
| A. | $\frac{3}{4}π{a}^{2}$ | B. | 3πa2 | C. | 6πa2 | D. | $\frac{3}{2}π{a}^{2}$ |