题目内容
20.已知a>0且a≠1,函数f(x)=loga(x2-ax+$\frac{1}{2}$)有最小值,则实数a的取值范围是( )| A. | (0,1) | B. | (0,1)∪(1,$\sqrt{2}$) | C. | (1,$\sqrt{2}$) | D. | ($\sqrt{2}$,+∞) |
分析 利用二次函数性质得出u(x)的最小值为:$\frac{1}{2}-\frac{{a}^{2}}{4}$,根据对数函数的单调性得出$\left\{\begin{array}{l}{a>1}\\{\frac{1}{2}-\frac{{a}^{2}}{4}>0}\end{array}\right.$,求解即可.
解答 解:∵u(x)=x2$-ax+\frac{1}{2}$=(x-$\frac{a}{2}$)2$+\frac{1}{2}$$-\frac{{a}^{2}}{4}$,
∴u(x)的最小值为:$\frac{1}{2}-\frac{{a}^{2}}{4}$.
∵,函数f(x)=loga(x2-ax+$\frac{1}{2}$)有最小值,
∴$\left\{\begin{array}{l}{a>1}\\{\frac{1}{2}-\frac{{a}^{2}}{4}>0}\end{array}\right.$,
即1$<a<\sqrt{2}$,
故选:C.
点评 本题考查了二次函数,与对数函数的单调性,解不等式解决问题,属于容易题,

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
11.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)与直线y=2x有交点,则双曲线离心率的取值范围是( )
| A. | ($\sqrt{5}$,+∞) | B. | [$\sqrt{5}$,+∞) | C. | (1,$\sqrt{5}$)∪($\sqrt{5}$,+∞) | D. | (1,$\sqrt{5}$) |
8.设i是虚数单位,则复数$\frac{1-3i}{i^3}$等于( )
| A. | -3+i | B. | -3-i | C. | 3+i | D. | 3-i |
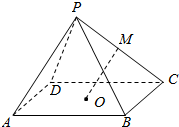 如图,在四棱锥P-ABCD中,底面是正方形,中心为O,且底面边长和侧棱长相等,M是PC的中点,求MO与AB所成的角.
如图,在四棱锥P-ABCD中,底面是正方形,中心为O,且底面边长和侧棱长相等,M是PC的中点,求MO与AB所成的角.