题目内容
15.已知一个正方体的各顶点都在同一个球面上,现用一个平面去截这个球和正方体,得到的截面图形刚好是一个圆及内接正三角形.若此正三角形的边长为a,则这个球的表面积为 ( )| A. | $\frac{3}{4}π{a}^{2}$ | B. | 3πa2 | C. | 6πa2 | D. | $\frac{3}{2}π{a}^{2}$ |
分析 确定正三角形的边长为a,可得正方体的对角线长为$\frac{\sqrt{6}}{2}$a,球的半径为$\frac{\sqrt{6}}{4}$a,即可求出这个球的表面积.
解答 解:由题意,正三角形的边长为a,
∴正方体的棱长为$\frac{\sqrt{2}}{2}$a,
∴正方体的对角线长为$\frac{\sqrt{6}}{2}$a,
∴球的半径为$\frac{\sqrt{6}}{4}$a,
∴这个球的表面积为4π×($\frac{\sqrt{6}}{4}$a)2=$\frac{3}{2}$πa2,
故选:D.
点评 本题考查球的表面积,考查学生的计算能力,确定球的半径是关键.

练习册系列答案
相关题目
3.若平面α的斜线l在α上的射影为l′,直线b∥α且b⊥l′,则b与l( )
| A. | 必相交 | B. | 必为异面直线 | C. | 垂直 | D. | 无法确定 |
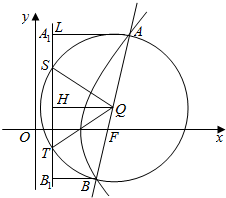 以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证:
以圆锥曲线的焦点弦AB为直径作圆,与相应准线l有两个不同的交点,求证: