题目内容
【题目】已知椭圆C以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为![]() ,点
,点![]() 在椭圆上,
在椭圆上,
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程.
求椭圆C的方程.
![]() Ⅱ
Ⅱ![]() 斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
斜率为k的直线l过点F且不与坐标轴垂直,直线l交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.
【答案】![]() Ⅰ
Ⅰ![]()
![]() .
.![]() Ⅱ
Ⅱ![]() .
.
【解析】
![]() Ⅰ
Ⅰ![]() 设椭圆方程为
设椭圆方程为![]() ,由椭圆可得
,由椭圆可得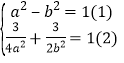 ,解出即可得出.
,解出即可得出.
![]() Ⅱ
Ⅱ![]() 解法一:设
解法一:设![]() ,
,![]() ,AB中点
,AB中点![]() ,直线AB的方程为
,直线AB的方程为![]() ,代入椭圆方程可得
,代入椭圆方程可得![]() ,利用根与系数的关系、中点坐标公式可得N的坐标,可得AB的垂直平分线NG的方程为,进而得出.
,利用根与系数的关系、中点坐标公式可得N的坐标,可得AB的垂直平分线NG的方程为,进而得出.
解法二:设![]() ,
,![]() ,AB中点
,AB中点![]() ,把点A,B的坐标分别代入椭圆方程相减可得:
,把点A,B的坐标分别代入椭圆方程相减可得:![]() ,利用中点坐标公式、斜率计算公式可得斜率
,利用中点坐标公式、斜率计算公式可得斜率![]() ,又
,又![]() ,可得
,可得![]() ,又
,又![]() 在椭圆内,即
在椭圆内,即![]() ,可得
,可得![]() ,利用AB的垂直平分线为
,利用AB的垂直平分线为![]() ,即可得出.
,即可得出.
![]() Ⅰ
Ⅰ![]() 设椭圆方程为
设椭圆方程为![]() ,
,
则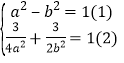
由![]() 得
得![]()
由![]() 得
得![]() 代入
代入![]() 得
得![]() ,
,
即![]() ,即
,即![]() ,或
,或![]()
![]() ,
,![]() ,得
,得![]() ,
,
![]() ,
,![]() ,
,
![]() 椭圆方程为
椭圆方程为![]() .
.
![]() Ⅱ
Ⅱ![]() 解法一:设
解法一:设![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
直线AB的方程为![]() ,
,
代入![]() ,整理得
,整理得![]() ,
,
![]() 直线AB过椭圆的左焦点F,
直线AB过椭圆的左焦点F,![]() 方程有两个不等实根,
方程有两个不等实根,
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 的垂直平分线NG的方程为
的垂直平分线NG的方程为![]() ,
,
![]() 时,
时,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
解法二:设![]() ,
,![]() ,AB中点
,AB中点![]() ,
,
由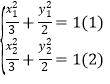 ,
,![]() 得
得![]() ,
,
斜率![]() ,
,
又![]() ,
,![]() ,
,
![]() ,得
,得![]() ,
,
![]() 在椭圆内,即
在椭圆内,即![]() ,
,
将![]() 代入得
代入得![]() ,
,
解得![]()
![]() ,
,
则AB的垂直平分线为![]() ,
,![]() 时,
时,![]() .
.

练习册系列答案
相关题目
【题目】在某学校进行的一次语文与历史成绩中,随机抽取了25位考生的成绩进行分析,25位考生的语文成绩已经统计在茎叶图中,历史成绩如下:
(Ⅰ)请根据数据在茎叶图中完成历史成绩统计;
(Ⅱ)请根据数据完成语文成绩的频数分布表及语文成绩的频率分布直方图;
语文成绩的频数分布表:
语文成绩分组 | [50,60) | [60,70) | [70,80) | [90,100) | [100,110) | [110,120] |
频数 |
