Question

【题目】已知命题p：x0∈[0，2]，log2（x+2）＜2m；命题q：关于x的方程3x2﹣2x+m2=0有两个相异实数根．
（1）若（￢p）∧q为真命题，求实数m的取值范围；
（2）若p∨q为真命题，p∧q为假命题，求实数m的取值范围．

Answer 1

【答案】
（1）解：令f（x）=log2（x+2），则f（x）在[0，2]上是增函数，

故当x∈[0，2]时，f（x）最小值为f（0）=1，故若p为真，则2m＞1， ．

△=4﹣12m2＞0即 时，方程3x2﹣2x+m2=0有两相异实数根，

∴

若（p）∧q为真，则实数m满足 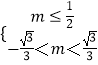故 ，

即实数m的取值范围为

（2）解：若p∨q为真命题，p∧q为假命题，则p、q一真一假，

若p真q假，则实数m满足 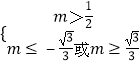即 ；

若p假q真，则实数m满足 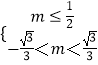即 ．

综上所述，实数m的取值范围为

【解析】（1）若（p）∧q为真，则实数m满足 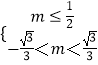故 ，解得实数m的取值范围；（2）若p∨q为真命题，p∧q为假命题，则p、q一真一假，分类讨论，可得实数m的取值范围．
【考点精析】关于本题考查的命题的真假判断与应用，需要了解两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系才能得出正确答案．