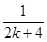题目内容
用数学归纳法证明不等式: >1(n∈N*且n>1).
>1(n∈N*且n>1).
 >1(n∈N*且n>1).
>1(n∈N*且n>1).见解析
①当n=2时,左边=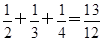 >1,
>1,
∴n=2时不等式成立;
②假设当n=k(k≥2)时不等式成立,即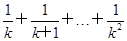 >1,
>1,
那么当n=k+1时,
左边=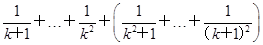
=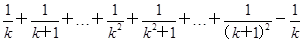
>1+(2k+1)·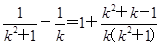 >1.
>1.
综上,对于任意n∈N*,n>1不等式均成立,原命题得证.
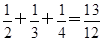 >1,
>1,∴n=2时不等式成立;
②假设当n=k(k≥2)时不等式成立,即
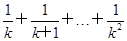 >1,
>1,那么当n=k+1时,
左边=
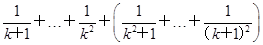
=
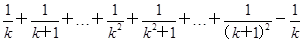
>1+(2k+1)·
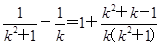 >1.
>1.综上,对于任意n∈N*,n>1不等式均成立,原命题得证.

练习册系列答案
相关题目
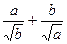 ≥
≥ .
. 成立.
成立.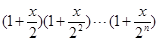 的展开式中,
的展开式中,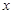 的系数为
的系数为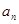 ,
,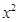 的系数为
的系数为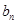 ,其中
,其中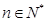
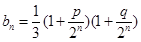 ,对
,对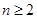 恒成立?证明你的结论.
恒成立?证明你的结论. ;
;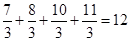 ;
; ;……
;…… 且
且 时,
时, .(最后结果用
.(最后结果用 表示)
表示)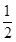 +
+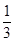 -
-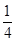 +…+
+…+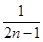 -
-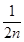 ,则ak+1等于( )
,则ak+1等于( )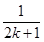
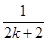 -
-