题目内容
已知a,b为正数,求证: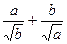 ≥
≥ .
.
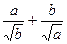 ≥
≥ .
.证明略
1:∵ a>0,b>0,
∴ ≥
≥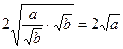 ,
,
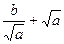 ≥
≥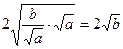 ,
,
两式相加,得
 ≥
≥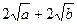 ,
,
∴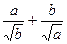 ≥
≥ .
.
解析2. ≥
≥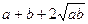
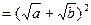 .
.
∴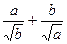 ≥
≥ .
.
解析3.∵a>0,b>0,∴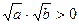 ,
,
∴欲证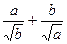 ≥
≥ ,
,
即证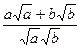 ≥
≥ ,
,
只要证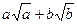 ≥
≥ ,
,
只要证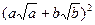 ≥
≥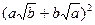 ,
,
即证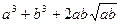 ≥
≥ ,
,
只要证a3+b3≥ab(a+b),
只要证a2+b2-ab≥ab,
即证(a-b)2≥0.
∵ (a-b)2≥0成立,∴原不等式成立.
【名师指引】当要证明的不等式形式上比较复杂时,常通过分析法寻求证题思路.
“分析法”与“综合法”是数学推理中常用的思维方法,特别是这两种方法的综合运用能力,对解决实际问题有重要的作用.这两种数学方法是高考考查的重要数学思维方法.
∴
 ≥
≥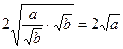 ,
,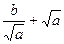 ≥
≥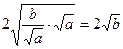 ,
,两式相加,得
 ≥
≥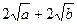 ,
,∴
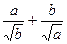 ≥
≥ .
.解析2.
 ≥
≥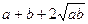
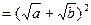 .
.∴
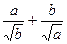 ≥
≥ .
.解析3.∵a>0,b>0,∴
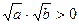 ,
,∴欲证
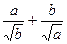 ≥
≥ ,
,即证
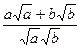 ≥
≥ ,
,只要证
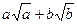 ≥
≥ ,
,只要证
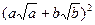 ≥
≥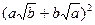 ,
,即证
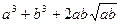 ≥
≥ ,
,只要证a3+b3≥ab(a+b),
只要证a2+b2-ab≥ab,
即证(a-b)2≥0.
∵ (a-b)2≥0成立,∴原不等式成立.
【名师指引】当要证明的不等式形式上比较复杂时,常通过分析法寻求证题思路.
“分析法”与“综合法”是数学推理中常用的思维方法,特别是这两种方法的综合运用能力,对解决实际问题有重要的作用.这两种数学方法是高考考查的重要数学思维方法.

练习册系列答案
相关题目
 ≥4
≥4 ;
; ≥( );a3b3+
≥( );a3b3+ ≥( );
≥( ); >1(n∈N*且n>1).
>1(n∈N*且n>1). +
+ +
+ ≥
≥ 
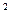 +b
+b +
+ +
+ ≥1
≥1
 的单调区间;
的单调区间;
 (
( )时,从“n=
)时,从“n= ”到“n=
”到“n= ”的证明,左边需增添的代数式是___________.
”的证明,左边需增添的代数式是___________.  z2≥2(xy+yz+zx)
z2≥2(xy+yz+zx) ≥2(
≥2( )
)