题目内容
已知数列{an}满足a1=1,且4an+1-anan+1+2an=9(n∈N?).
(1)求a2,a3,a4的值;
(2)由(1)猜想{an}的通项公式,并给出证明.
(1)求a2,a3,a4的值;
(2)由(1)猜想{an}的通项公式,并给出证明.
(1)a2=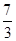 ,a3=
,a3=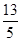 ,a4=
,a4=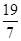 (2)an=
(2)an=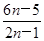
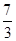 ,a3=
,a3=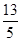 ,a4=
,a4=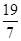 (2)an=
(2)an=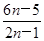
(1)由4an+1-anan+1+2an=9,得an+1=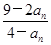 =2-
=2-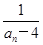 ,求得a2=
,求得a2=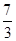 ,a3=
,a3=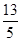 ,a4=
,a4=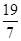 .
.
(2)猜想an=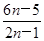 .证明:①当n=1时,猜想成立.
.证明:①当n=1时,猜想成立.
②设当n=k时(k∈N*)时,猜想成立,即ak=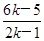 ,
,
则当n=k+1时,有ak+1=2-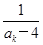 =2-
=2-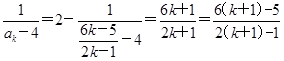 ,所以当n=k+1时猜想也成立.
,所以当n=k+1时猜想也成立.
综合①②,猜想对任何n∈N*都成立.
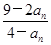 =2-
=2-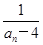 ,求得a2=
,求得a2=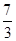 ,a3=
,a3=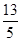 ,a4=
,a4=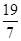 .
.(2)猜想an=
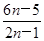 .证明:①当n=1时,猜想成立.
.证明:①当n=1时,猜想成立.②设当n=k时(k∈N*)时,猜想成立,即ak=
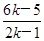 ,
,则当n=k+1时,有ak+1=2-
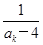 =2-
=2-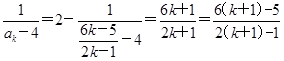 ,所以当n=k+1时猜想也成立.
,所以当n=k+1时猜想也成立.综合①②,猜想对任何n∈N*都成立.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中,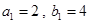 ,且
,且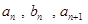 成等差数列,
成等差数列,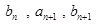 成等比数列
成等比数列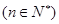 .
.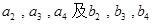 ;
; >1(n∈N*且n>1).
>1(n∈N*且n>1).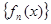 满足:
满足: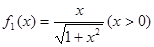 ,
,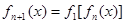
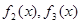 ;
;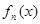 的表达式,并证明你的结论.
的表达式,并证明你的结论.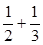 +…+
+…+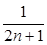 (n∈N*)中,当n=1时式子值为1+
(n∈N*)中,当n=1时式子值为1+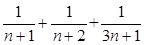 (n∈N*),则f(k+1)=f(k)+
(n∈N*),则f(k+1)=f(k)+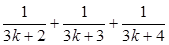
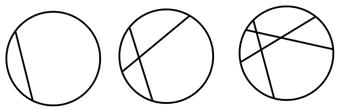
 条两两相交的弦,把圆最多分成 部分.
条两两相交的弦,把圆最多分成 部分.