题目内容
19.设曲线y=x2+1在点(x,f(x))处的切线的斜率为g(x),则函数y=g(x)cosx的部分图象可以为( )| A. | 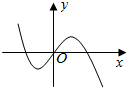 | B. | 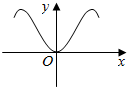 | C. |  | D. | 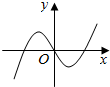 |
分析 先研究函数y=g(x)cosx的奇偶性,再根据在某点处的函数值的符号进一步进行判定.
解答 解:g(x)=2x,g(x)•cosx=2x•cosx,
g(-x)=-g(x),cos(-x)=cosx,
∴y=g(x)cosx为奇函数,排除B、D.
令x=0.1>0.
故选:A.
点评 本题主要考查了导数的运算,以及考查学生识别函数的图象的能力,属于基础题.

练习册系列答案
相关题目
7.如图是计算1+2+4+…+219的值的一个程序框图,则其中空白判断框内应填入的是( )
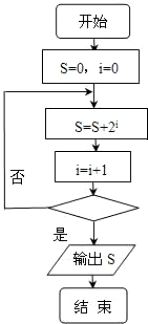

| A. | i=19 | B. | i≥20 | C. | i≤19 | D. | i≤20 |
4.在研究高血压与患心脏病的关系调查中,调查了有高血压者30人,其中有20人患心脏病;调查的80个不高血压者中有30人患心脏病,
(1)根据以上数据建立一个2×2的列联表;
(2)若认为“高血压与患心脏病有关”,则出错的概率会是多少?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;n=a+b+c+d
(1)根据以上数据建立一个2×2的列联表;
(2)若认为“高血压与患心脏病有关”,则出错的概率会是多少?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;n=a+b+c+d
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
11.函数 f(x)=(x-2014)(x+2015)的图象与x轴,y轴有三个交点,有一个圆恰经过这三个点,则此圆与坐标轴的另一个交点是( )
| A. | (0,-1) | B. | (0,1) | C. | (0,$\sqrt{2014×2015}$) | D. | (0,$\sqrt{\frac{2014}{2015}}$) |
8.运行如图程序,若输入的是-2,则输出的结果是( )


| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
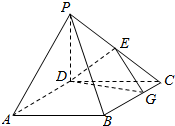 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB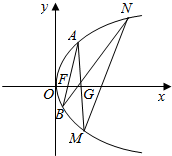 如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).
如图,已知抛物线C:y2=2px(p>0),焦点为F,过点G(p,0)作直线l交抛物线C于A,M两点,设A(x1,y1),M(x2,y2).