题目内容
18.若向由f(x)=|x|+2表示的曲线与直线y=3围成的三角形内随机投掷一粒黄豆,求黄豆与点(0,2)的距离小于1的概率.分析 由题意,画出图形,分别求出区域的面积,利用面积比求概率.
解答 解:由题意,f(x)=|x|+2表示的曲线与直线y=3围成的三角形如图,与点(0,2)的距离小于1的部分如图阴影部分,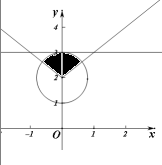
由几何概型公式可得黄豆与点(0,2)的距离小于1的概率为$\frac{\frac{1}{4}π}{\frac{1}{2}×2×1}=\frac{π}{4}$.
点评 本题考查了几何概型概率求法;关键是名称事件集合的测度为区域的面积.

练习册系列答案
相关题目
8.若不等式ex≥kx-k对x>1恒成立,则实数k的最大值是( )
| A. | e2 | B. | e | C. | $\frac{1}{e}$ | D. | 1 |
3.若某公司从四位大学毕业生甲、乙、丙、丁中录用两人,这四人被录用的机会均等,则甲被录用的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
7.如图是计算1+2+4+…+219的值的一个程序框图,则其中空白判断框内应填入的是( )
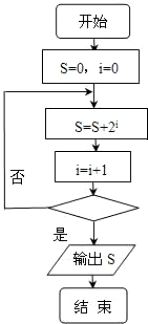

| A. | i=19 | B. | i≥20 | C. | i≤19 | D. | i≤20 |
8.运行如图程序,若输入的是-2,则输出的结果是( )


| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
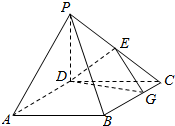 如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB
如图,四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为正方形,BC=PD=2,E为PC的中点,G在BC上,且CG=$\frac{1}{3}$CB