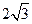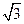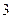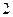题目内容
(本题满分18分,第(1)小题4分,第(2)小题6分,第(2)小题8分)
已知双曲线C: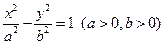 的一个焦点是
的一个焦点是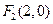 ,且
,且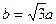 。
。
(1)求双曲线C的方程;
(2)设经过焦点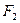 的直线
的直线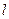 的一个法向量为
的一个法向量为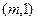 ,当直线
,当直线
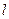 与双曲线C的右支相交于
与双曲线C的右支相交于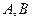 不同的两点时,求实数
不同的两点时,求实数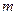 的取值范围;并证明
的取值范围;并证明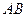 中点
中点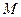 在曲线
在曲线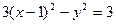 上。
上。
(3)设(2)中直线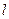 与双曲线C的右支相交于
与双曲线C的右支相交于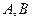 两点,问是否存在实数
两点,问是否存在实数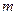 ,使得
,使得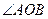 为锐角?若存在,请求出
为锐角?若存在,请求出 的范围;若不存在,请说明理由。
的范围;若不存在,请说明理由。
已知双曲线C:
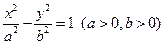 的一个焦点是
的一个焦点是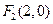 ,且
,且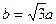 。
。(1)求双曲线C的方程;
(2)设经过焦点
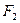 的直线
的直线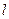 的一个法向量为
的一个法向量为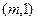 ,当直线
,当直线
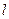 与双曲线C的右支相交于
与双曲线C的右支相交于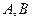 不同的两点时,求实数
不同的两点时,求实数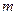 的取值范围;并证明
的取值范围;并证明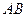 中点
中点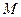 在曲线
在曲线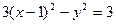 上。
上。(3)设(2)中直线
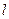 与双曲线C的右支相交于
与双曲线C的右支相交于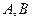 两点,问是否存在实数
两点,问是否存在实数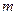 ,使得
,使得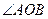 为锐角?若存在,请求出
为锐角?若存在,请求出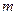 的范围;若不存在,请说明理由。
的范围;若不存在,请说明理由。(1)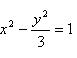 (2)略 (3)略
(2)略 (3)略
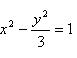 (2)略 (3)略
(2)略 (3)略(1)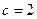
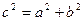
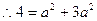
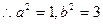
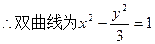 。 ……………………………………4分
。 ……………………………………4分
(2)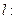
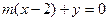 由
由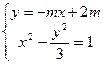 得
得
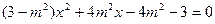
由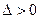 得
得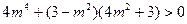
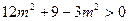
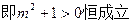
……………………………………6分
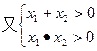
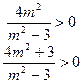
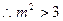
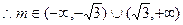
……………………………………8分
设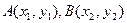 ,则
,则
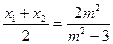
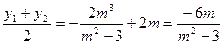
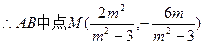 …………………………
………………………… …………10分
…………10分
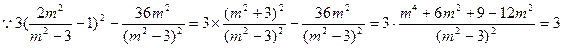
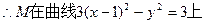 。 ……………………………………12分
。 ……………………………………12分
(3)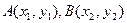 ,
, 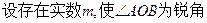 ,
,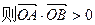
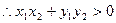 ………………
……………… ……………………14分
……………………14分
因为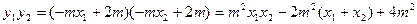
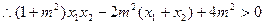 ……………………………………16分
……………………………………16分
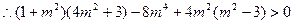 即
即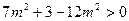
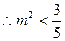 ,
, 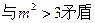
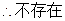
……………………………………18分
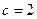
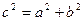
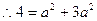
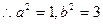
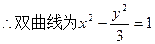 。 ……………………………………4分
。 ……………………………………4分(2)
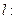
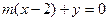 由
由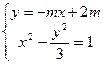 得
得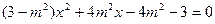
由
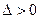 得
得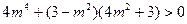
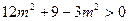
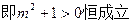
……………………………………6分
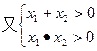
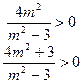
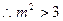
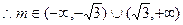
……………………………………8分
设
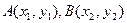 ,则
,则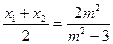
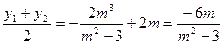
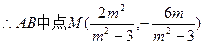 …………………………
………………………… …………10分
…………10分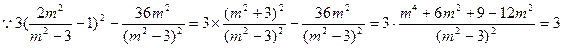
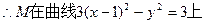 。 ……………………………………12分
。 ……………………………………12分(3)
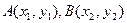 ,
, 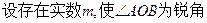 ,
,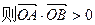
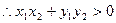 ………………
……………… ……………………14分
……………………14分因为
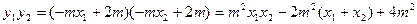
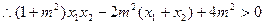 ……………………………………16分
……………………………………16分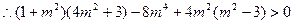 即
即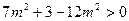
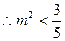 ,
, 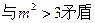
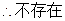
……………………………………18分

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
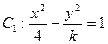 按向量
按向量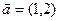 平移后得到曲线
平移后得到曲线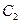 ,曲线
,曲线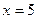 ,则
,则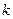 的值为____________,离心率
的值为____________,离心率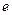 为_________.
为_________.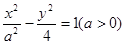 的右焦点与抛物线
的右焦点与抛物线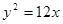 的焦点重合,则该双曲线的离心率为 ( )
的焦点重合,则该双曲线的离心率为 ( )



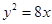 的焦点到双曲线
的焦点到双曲线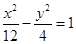 的渐近线的距离为( )
的渐近线的距离为( )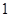
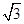
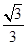
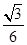
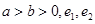 分别是圆锥曲线
分别是圆锥曲线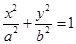 和
和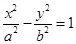 的离心率,设
的离心率,设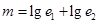 ,则
,则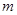 的取值范围是
的取值范围是 ,0)
,0) )
)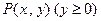 到定点
到定点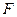
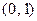 的距离比它到
的距离比它到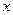 轴的距离大1,记点
轴的距离大1,记点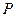 的轨迹为曲线
的轨迹为曲线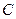 .
.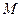 过
过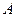
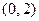 ,且圆心
,且圆心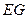 是圆
是圆 是否为定值?为什么?
是否为定值?为什么?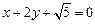 与圆
与圆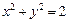 相交于
相交于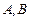 两点,
两点,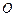 为原点,则
为原点,则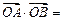 .
.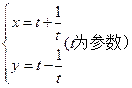 上的点是( )
上的点是( )
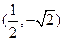 B
B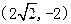 C
C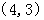 D
D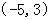
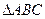 中,
中,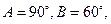 一椭圆与一双曲线都以
一椭圆与一双曲线都以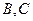 为焦点,且都过
为焦点,且都过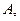 它们的离心率分别为
它们的离心率分别为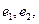 则
则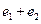 的值为( )
的值为( )