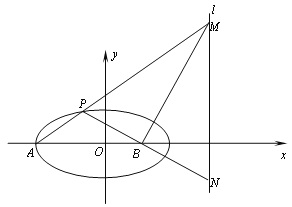
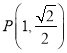题目内容
【题目】已知椭圆C: ![]() =1(a>b>0)过点A(﹣
=1(a>b>0)过点A(﹣ ![]() ,
, ![]() ),离心率为
),离心率为 ![]() ,点F1 , F2分别为其左右焦点.
,点F1 , F2分别为其左右焦点.
(1)求椭圆C的标准方程;
(2)若y2=4x上存在两个点M,N,椭圆上有两个点P,Q满足,M,N,F2三点共线,P,Q,F2三点共线,且PQ⊥MN.求四边形PMQN面积的最小值.
【答案】
(1)解:由题意得: ![]() ,a2﹣b2=c2,得b=c,
,a2﹣b2=c2,得b=c,
因为椭圆过点A(﹣ ![]() ,
, ![]() ),
),
则 ![]() +
+ ![]() =1,
=1,
解得c=1,所以a2=2,
所以椭圆C方程为 ![]()
(2)解:当直线MN斜率不存在时,直线PQ的斜率为0,
易得 ![]() ,
, ![]() .
.
当直线MN斜率存在时,设直线方程为:y=k(x﹣1)(k≠0)
与y2=4x联立得k2x2﹣(2k2+4)x+k2=0,
令M(x1,y1),N(x2,y2),则 ![]() ,x1x2=1,
,x1x2=1,
|MN|= ![]()
![]() .即有
.即有 ![]() ,
,
∵PQ⊥MN,∴直线PQ的方程为:y=﹣ ![]() (x﹣1),
(x﹣1),
将直线与椭圆联立得,(k2+2)x2﹣4x+2﹣2k2=0,
令P(x3,y3),Q(x4,y4),x3+x4= ![]() ,x3x4=
,x3x4= ![]() ,
,
由弦长公式|PQ|= ![]()
![]() ,
,
代入计算可得 ![]() ,
,
∴四边形PMQN的面积S= ![]() |MN||PQ|=
|MN||PQ|= ![]() ,
,
令1+k2=t,(t>1),
上式 ![]() =
= ![]()
![]() ,
,
所以 ![]() .最小值为
.最小值为 ![]()
【解析】(1)由椭圆的离心率公式和点满足椭圆方程及a,b,c的关系,解方程,即可得到椭圆方程;(2)讨论直线MN的斜率不存在,求得弦长,求得四边形的面积;当直线MN斜率存在时,设直线方程为:y=k(x﹣1)(k≠0)联立抛物线方程和椭圆方程,运用韦达定理和弦长公式,以及四边形的面积公式,计算即可得到最小值.

【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.