题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )经过点
)经过点 ,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
,且两焦点与短轴的一个端点的连线构成等腰直角三角形.
(1)求椭圆的方程;
(2)动直线![]() :
: ![]() (
(![]() ,
, ![]() )交椭圆
)交椭圆![]() 于
于![]() 、
、![]() 两点,试问:在坐标平面上是否存在一个定点
两点,试问:在坐标平面上是否存在一个定点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() .若存在,求出点
.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)在坐标平面上存在一个定点
;(2)在坐标平面上存在一个定点![]() 满足条件.
满足条件.
【解析】试题分析:
(1)由题设知a= ![]() ,所以
,所以 ![]() ,椭圆经过点P(1,
,椭圆经过点P(1, ![]() ),代入可得b=1,a=
),代入可得b=1,a=![]() ,由此可知所求椭圆方程
,由此可知所求椭圆方程
(2)首先求出动直线过(0,﹣![]() )点.当l与x轴平行时,以AB为直径的圆的方程:x2+(y+
)点.当l与x轴平行时,以AB为直径的圆的方程:x2+(y+![]() )2=
)2=![]() ;当l与y轴平行时,以AB为直径的圆的方程:x2+y2=1.由
;当l与y轴平行时,以AB为直径的圆的方程:x2+y2=1.由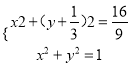 .由此入手可求出点T的坐标.
.由此入手可求出点T的坐标.
解:
(1)∵椭圆![]() :
: ![]() (
(![]() )的两焦点与短轴的一个端点的连线构成等腰直角三角形,
)的两焦点与短轴的一个端点的连线构成等腰直角三角形,
∴![]() ,∴
,∴![]()
又∵椭圆经过点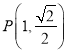 ,代入可得
,代入可得![]() .
.
∴![]() ,故所求椭圆方程为
,故所求椭圆方程为![]() .
.
(2)首先求出动直线过![]() 点.
点.
当![]() 与
与![]() 轴平行时,以
轴平行时,以![]() 为直径的圆的方程:
为直径的圆的方程: ![]()
当![]() 与
与![]() 轴平行时,以
轴平行时,以![]() 为直径的圆的方程:
为直径的圆的方程: ![]()
由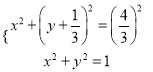 解得
解得![]()
即两圆相切于点![]() ,因此,所求的点
,因此,所求的点![]() 如果存在,只能是
如果存在,只能是![]() ,事实上,点
,事实上,点![]() 就是所求的点.
就是所求的点.
证明如下:
当直线![]() 垂直于
垂直于![]() 轴时,以
轴时,以![]() 为直径的圆过点
为直径的圆过点![]()
当直线![]() 不垂直于
不垂直于![]() 轴,可设直线
轴,可设直线![]() :
: ![]()
由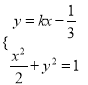 消去
消去![]() 得:
得: ![]()
记点![]() 、
、![]() ,则
,则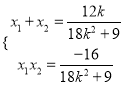
又因为![]() ,
, ![]()
所以![]()
![]()
![]()
![]()
![]()
所以![]() ,即以
,即以![]() 为直径的圆恒过点
为直径的圆恒过点![]()
所以在坐标平面上存在一个定点![]() 满足条件.
满足条件.

【题目】某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在[29.94,30.06)的零件为优质品.从两个分厂生产的零件中各抽出了500件,量其内径尺寸,得结果如下表:
甲厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 12 | 63 | 86 | 182 | 92 | 61 | 4 |
乙厂:
分组 | [29.86,29.90) | [29.90,29.94) | [29.94,29.98) | [29.98,30.02) | [30.02,30.06) | [30.06,30.10) | [30.10,30.14) |
频数 | 29 | 71 | 85 | 159 | 76 | 62 | 18 |
(1)试分别估计两个分厂生产的零件的优质品率;
(2)由以上统计数据填下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“两个分厂生产的零件的质量有差异”.
的把握认为“两个分厂生产的零件的质量有差异”.
甲 厂 | 乙 厂 | 合计 | |
优质品 | |||
非优质品 | |||
合计 |
附: 
|
|
|
|
|
|
|
|
|
|