题目内容
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,且过点(1,
,且过点(1,![]() ).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
).过椭圆C的左顶点A作直线交椭圆C于另一点P,交直线l:x=m(m>a)于点M.已知点B(1,0),直线PB交l于点N.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若MB是线段PN的垂直平分线,求实数m的值.

【答案】(1)![]() +y2=1(2)
+y2=1(2)![]()
【解析】试题分析:(1)根据题意列出关于![]() 、
、![]() 、
、![]() 的方程组,结合性质
的方程组,结合性质![]() ,
,![]() ,求出
,求出![]() 、
、![]() 、
、![]() ,即可得结果;(2)设
,即可得结果;(2)设![]() ,则
,则![]() ,所以
,所以![]() .可得直线
.可得直线![]() 的方程为
的方程为![]() ,根据
,根据![]() 可得
可得![]() ,解方程即可得结果.
,解方程即可得结果.
试题解析:(1)因为椭圆C的离心率为![]() ,所以a2=4b2.
,所以a2=4b2.
又因为椭圆C过点(1,![]() ),所以
),所以![]() +
+![]() =1,
=1,
解得a2=4,b2=1.
所以椭圆C的方程为![]() +y2=1.
+y2=1.
(2)解法1
设P(x0,y0),-2<x0<2, x0≠1,则![]() +y02=1.
+y02=1.
因为MB是PN的垂直平分线,所以P关于B的对称点N(2-x0,-y0),
所以2-x0=m.
由A(-2,0),P(x0,y0),可得直线AP的方程为y=![]() (x+2),
(x+2),
令x=m,得y=![]() ,即M(m,
,即M(m,![]() ).
).
因为PB⊥MB,所以kPB·kMB=-1,
所以kPB·kMB=![]() ·
·![]() =-1,
=-1,
即![]() =-1.
=-1.
因为![]() +y02=1.所以
+y02=1.所以![]() =1.
=1.
因为x0=2-m ,所以化简得3m2-10m+4=0,
解得m=![]() .
.
因为m>2,所以m=![]() .
.
解法2
①当AP的斜率不存在或为0时,不满足条件.
②设AP斜率为k,则AP:y=k(x+2),
联立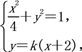 消去y得(4k2+1)x2+16k2x+16k2-4=0.
消去y得(4k2+1)x2+16k2x+16k2-4=0.
因为xA=-2,所以xP=![]() ,所以yP=
,所以yP=![]() ,
,
所以P(![]() ,
,![]() ).
).
因为PN的中点为B,所以m=2-![]() =
=![]() .(*)
.(*)
因为AP交直线l于点M,所以M(m,k(m+2)),
因为直线PB与x轴不垂直,所以![]() ≠1,即k2≠
≠1,即k2≠![]() ,
,
所以kPB= =
=![]() ,kMB=
,kMB=![]() .
.
因为PB⊥MB,所以kPB·kMB=-1,
所以![]() ·
·![]() =-1.(**)
=-1.(**)
将(*)代入(**),化简得48k4-32k2+1=0,
解得k2=![]() ,所以m=
,所以m=![]() =
=![]() .
.
又因为m>2,所以m=![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案