题目内容
4．|z-5+12i|≤2，则|z|的最小值为（ ）| A． | 7 | B． | 9 | C． | 11 | D． | 15 |
分析 根据复数的几何意义，利用数形结合进行求解即可．
解答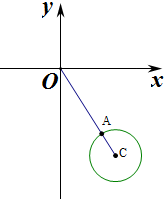 
解：由|z-5+12i|≤2得|z-（5-12i）|≤2，
则z的几何意义为以C（5，-12）为圆心，半径为2的圆及圆的内部，
则对应的图象为：
则|z|的几何意义为区域内的点到圆的距离，
则由图象知|z|的最小值为|OA|=|OC|-2=$\sqrt{{5}^{2}+（-12）^{2}}$-2=13-2=11，
故选：C
点评 本题主要考查复数的几何意义的应用，利用数形结合是解决本题的关键．
练习册系列答案
相关题目
9．
生物兴趣小组的同学到野外调查某种植物的生长情况，共测量了k∈Z株该植物的高度（单位：厘米），获得数据如下：
6，7，8，9，10，14，16，17，17，18，19，20，20，21，24，26，26，27，28，29，29，30，30，30，31，31，33，36，37，41．
根据上述数据得到样本的频率分布表如下：
（1）确定样本频率分布表中n1，n2，f1和f2的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）用（2）的频率分布直方图估计该植物生长高度的平均值．
生物兴趣小组的同学到野外调查某种植物的生长情况，共测量了k∈Z株该植物的高度（单位：厘米），获得数据如下：6，7，8，9，10，14，16，17，17，18，19，20，20，21，24，26，26，27，28，29，29，30，30，30，31，31，33，36，37，41．
根据上述数据得到样本的频率分布表如下：
| 分组 | 频数 | 频率 |
| [5，15] | 6 | 0.2 |
| （15，25] | 9 | 0.3 |
| （25，35] | n1 | f1 |
| （35，45] | n2 | f2 |
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）用（2）的频率分布直方图估计该植物生长高度的平均值．
12．函数y=sin2x的导数是（ ）
| A． | y=2sinx | B． | y=sin2x | C． | y=2sin2x | D． | y=2cosx |
9．若a+b=1，则恒有（ ）
| A． | ab≥$\frac{1}{4}$ | B． | ab≤$\frac{1}{4}$ | C． | $\frac{1}{ab}$≥4 | D． | a2+b2≥1 |
14．$|\vec a|=1，|\vec b|=2$则$\vec a$与$\vec b$的夹角为120°，则$（\vec a+2\vec b）•（2\vec a+\vec b）$的值为（ ）
| A． | -5 | B． | 5 | C． | $-\sqrt{5}$ | D． | $\sqrt{5}$ |