题目内容
1．
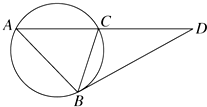过D作圆的切线切于B点，作割线交圆于A、C两点，若BD=3，AD=4，AB=2，则BC=$\frac{3}{2}$．
分析 根据圆的切割线定理，先求出DC，再根据△ABD∽△BCD 求出BC．
解答 解：由圆的切割线定理，得BD2=DC•DA，所以DC=$\frac{9}{4}$，
又△ABD∽△BCD，得$\frac{AB}{BC}=\frac{BD}{CD}$，代入数据计算得BC=$\frac{3}{2}$．
故答案为：$\frac{3}{2}$．
点评 本题考查了圆的切割线定理，考查三角形相似的判定与性质的运用，比较基础．
练习册系列答案
小学课时特训系列答案
相关题目
某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，年龄在第3组的人数是4．
12．函数y=sin2x的导数是（ ）
| A． | y=2sinx | B． | y=sin2x | C． | y=2sin2x | D． | y=2cosx |
9．若a+b=1，则恒有（ ）
| A． | ab≥$\frac{1}{4}$ | B． | ab≤$\frac{1}{4}$ | C． | $\frac{1}{ab}$≥4 | D． | a2+b2≥1 |
10．下列说法正确的是（ ）
| A． | 正切函数在定义域内为单调增函数 | |
| B． | 若α是第一象限角，则$\frac{α}{2}$是第一象限角 | |
| C． | 用秦九韶算法计算多项式f（x）=3x6+5x4+6x3-4x-5当x=3时的值时，v2=3v1+5=32 | |
| D． | 若扇形圆心角为2弧度，且扇形弧所对的弦长为2，则这个扇形的面积为$\frac{1}{{{{sin}^2}1}}$ |