题目内容
1．设向量$\overrightarrow{a}$=（1，3m-1，n-2），$\overrightarrow{b}$=（2，3m+1，3n-4），若$\overrightarrow{a}$∥$\overrightarrow{b}$，则$\overrightarrow{a}$$•\overrightarrow{b}$=18．分析 利用向量共线定理、数量积运算即可得出．
解答 解：∵$\overrightarrow{a}$∥$\overrightarrow{b}$，
∴存在实数λ使得$\overrightarrow{a}=λ\overrightarrow{b}$，
∴$\left\{\begin{array}{l}{1=2λ}\\{3m-1=λ（3m+1）}\\{n-2=λ（3n-4）}\end{array}\right.$，解得$λ=\frac{1}{2}$，m=1，n=0．
∴$\overrightarrow{a}$=（1，2，-2），$\overrightarrow{b}$=（2，4，-4），
∴$\overrightarrow{a}•\overrightarrow{b}$=2+8+8=18．
故答案为：18．
点评 本题考查了向量共线定理、数量积运算，属于基础题．
练习册系列答案
相关题目
11．与直线l：3x-4y+5=0平行且过点（-1，2）的直线方程为（ ）
| A． | 4x-3y+10=0 | B． | 4x-3y-11=0 | C． | 3x-4y-11=0 | D． | 3x-4y+11=0 |
9．
生物兴趣小组的同学到野外调查某种植物的生长情况，共测量了k∈Z株该植物的高度（单位：厘米），获得数据如下：
6，7，8，9，10，14，16，17，17，18，19，20，20，21，24，26，26，27，28，29，29，30，30，30，31，31，33，36，37，41．
根据上述数据得到样本的频率分布表如下：
（1）确定样本频率分布表中n1，n2，f1和f2的值；
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）用（2）的频率分布直方图估计该植物生长高度的平均值．
生物兴趣小组的同学到野外调查某种植物的生长情况，共测量了k∈Z株该植物的高度（单位：厘米），获得数据如下：6，7，8，9，10，14，16，17，17，18，19，20，20，21，24，26，26，27，28，29，29，30，30，30，31，31，33，36，37，41．
根据上述数据得到样本的频率分布表如下：
| 分组 | 频数 | 频率 |
| [5，15] | 6 | 0.2 |
| （15，25] | 9 | 0.3 |
| （25，35] | n1 | f1 |
| （35，45] | n2 | f2 |
（2）根据上述频率分布表，画出样本频率分布直方图；
（3）用（2）的频率分布直方图估计该植物生长高度的平均值．
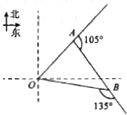如图，一只蜘蛛从点O出发沿北偏东45°方向爬行xcm，到达点A处捕捉到一只小虫，然后沿OA方向右转105°爬行10cm，到达点B处捕捉哦另一只小虫，这时他沿AB方向右转135°爬行回到它的出发点O处，那么x=$\frac{10\sqrt{6}}{3}$．
某企业员工500人参加“学雷锋”志愿活动，按年龄分组：第1组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50），得到的频率分布直方图如图所示．现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，年龄在第3组的人数是4．
13．函数y=x3+4x的递增区间是（ ）
| A． | （0，+∞） | B． | （-∞，-2） | C． | （2，+∞） | D． | （-∞，+∞） |
