已知z∈C.|z-(1+i)|=1.则|z+2+3i|的最小值为4．题目和参考答案——青夏教育精英家教网——

题目内容

16．已知z∈C，|z-（1+i）|=1，则|z+2+3i|的最小值为4．

分析由题意画出图形，数形结合求得|z+2+3i|的最小值．

解答解：由|z-（1+i）|=1，可得在复平面内z所对应点的轨迹为以（1，1）为圆心，以1为半径的圆，
如图，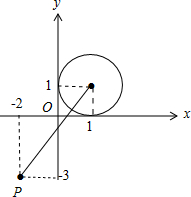

∴|z+2+3i|的最小值$\sqrt{（-2-1）^{2}+（-3-1）^{2}}-1=4$．
故答案为：4．

点评本题考查复数模的求法，考查了数形结合的解题思想方法，是基础题．

练习册系列答案

南方新课堂快乐暑假系列答案

百年学典快乐假期暑假作业系列答案

暑假提优40天系列答案

黄冈状元成才路状元作业本系列答案

1加1好成绩暑假作业沈阳出版社系列答案

快乐天天练暑假作业安徽师范大学出版社系列答案

欢乐岛暑假小小练系列答案

过好暑假每一天系列答案

暑假生活学习与生活系列答案

小学升初中衔接教材中南大学出版社系列答案

相关题目

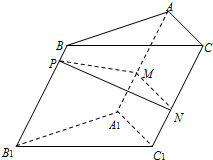如图，点P为斜三棱柱ABC-A₁B₁C₁的侧棱BB₁上一点，PM⊥BB₁交AA₁于点M，PN⊥BB₁交CC₁于点N．
（1）求证：CC₁⊥MN；
（2）在任意△DEF中有余弦定理：DE²=DF²+EF²-2DF•EFcos∠DFE．拓展到空间，类比三角形的余弦定理，写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式，并予以证明．
（3）在（2）中，我们看到了平面图形中的性质类比到空间图形的例子，这样的例子还有不少．下面请观察平面勾股定理的条件和结论特征，试着将勾股定理推广到空间去．

勾股定理的类比	三角形ABC	四面体O-ABC
条件	AB⊥AC	OA、OB、OC两两垂直
结论	AB²+AC²=BC²	？

请在答题纸上完成上表中的类比结论，并给出证明．

15．已知直线m，l，平面α，β，且m⊥α，l?β，给出下列命题：①若α∥β，则m⊥l； ②若α⊥β，则m∥l； ③若m⊥l，则α⊥β； ④若m∥l，则α⊥β．其中正确的命题的是（　　）

4．已知函数f（x）=lnx，g（x）=ax²-bx（a、b为常数）．
（1）求函数f（x）在点（1，f（1））处的切线方程；
（2）当函数g（x）在x=2处取得极值-2．求函数g（x）的解析式；
（3）当$a=\frac{1}{2}$时，设h（x）=f（x）+g（x），若函数h（x）在定义域上存在单调减区间，求实数b的取值范围．

11．已知f（x）=2sin（x-$\frac{π}{6}$）cos（x-$\frac{π}{6}$）+2．
（Ⅰ）求函数f（x）的最小正周期；
（Ⅱ）求函数f（x）的对称轴和对称中心．

1．请先阅读：在等式cos2x=2cos²x-1（x∈R）的两边求导，得（cos2x）′=（2cos²x-1）′，由求导法则，得（-sin2x）•2=4cosx•（-sinx），化简得等式：sin2x=2cosx•sinx，利用上面的想法（或其他方法），求和$\sum_{k=1}^{n}$3^k-1•k${C}_{n}^{k}$=n•4^n-1．

8．在数列{a_n}中，设a_n+1+3a_n=0，且a₁=-1，求{a_n}的通项公式和前n项和公式．

5．已知M，N为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右顶点，P（异于点M，N）是双曲线上任意一点，记直线PM，PN的斜率分别为k₁，k₂，则当e${\;}^{{k}_{1}}$${\;}^{{k}_{2}}$^-1-ln（k₁k₂）取最小值时，双曲线离心率为（　　）

6．两条直线2x+3y-k=0和x-ky+12=0的交点在直线y=-x上，那么k的值是（　　）