题目内容
6.两条直线2x+3y-k=0和x-ky+12=0的交点在直线y=-x上,那么k的值是( )| A. | -4 | B. | 3 | C. | 3或-4 | D. | ±4 |
分析 根据直线2x+3y-k=0和x-ky+12=0的交点在直线y=-x上,设出交点坐标,代入两直线方程,求出k的值.
解答 解:∵直线2x+3y-k=0和x-ky+12=0的交点在直线y=-x上,
∴设交点坐标为(m,-m),代入两直线方程,
得$\left\{\begin{array}{l}{2m-3m-k=0}\\{m+km+12=0}\end{array}\right.$,
消去m,得k2+k-12=0,
解得k=-4,或k=3;
∴k的值是3或-4.
故选:C.
点评 本题考查了求两条直线交点的应用问题,通常是由直线方程组成方程组,求出交点坐标,是基础题目.

练习册系列答案
相关题目
1.已知数列{an}满足$\frac{{a}_{n+1}+{a}_{n}-1}{{a}_{n+1}-{a}_{n}+1}$=n(n∈N*),且a4=28,则首项a1=1,通项公式an=(2n-1)n.
18.在等比数列{an}中,a1=5,q=1,则S6=( )
| A. | 5 | B. | 0 | C. | 不存在 | D. | 30 |
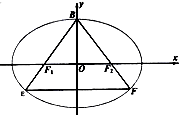 已知点B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点,F1,F2分别是椭圆的左右焦点,直线BF1,BF2与椭圆分别交于E,F两点,△BEF为等边三角形.
已知点B是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点,F1,F2分别是椭圆的左右焦点,直线BF1,BF2与椭圆分别交于E,F两点,△BEF为等边三角形.