题目内容
1.集合P={x|$\frac{x-1}{x+3}$>0},Q={x|y=$\sqrt{4-{x}^{2}}$},则P∩Q=( )| A. | (1,2] | B. | [1,2] | C. | (-∞,-3)∪(1,+∞) | D. | [1,2) |
分析 利用不等式的解法求出集合P,函数的定义域求出集合Q,然后求解交集即可.
解答 解:集合P={x|$\frac{x-1}{x+3}$>0}={x|x>1或x<-3},
Q={x|y=$\sqrt{4-{x}^{2}}$}={x|-2≤x≤2},
P∩Q={x|1<x≤2}=(1,2].
故选:A.
点评 本题考查集合的交集的求法,分式不等式的解法,考查计算能力.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
8.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b<c.在不同的方案中,最低的总费用(单位:元)是( )
| A. | ax+by+cz | B. | az+by+cx | C. | ay+bz+cx | D. | ay+bx+cz |
10.在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,点M为AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P、Q可以重合),则MP+PQ的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
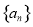 的公差为
的公差为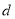 ,前
,前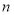 项和为
项和为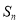 ,若
,若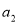 ,
,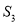 ,
,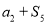 成等比数列,则
成等比数列,则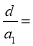 ( )
( )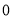 B.
B.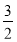
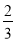 D.
D.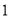
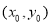 是直线
是直线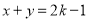 与圆
与圆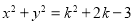 的公共点,则
的公共点,则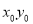 的取值范围是__________.
的取值范围是__________.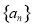 的公差为
的公差为 ,前
,前 项和为
项和为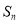 ,若
,若 ,
, ,
, 成等比数列,则
成等比数列,则 ( )
( ) B.
B.
 D.
D.