题目内容

9．已知在等比数列{an}中，若q=2，S8=6，则a17+a18+a19+a20的值是$\frac{3•{2}^{17}}{17}$．

分析 设出等比数列的首项，由题意列式求出首项，再由等比数列的前n项和得答案．

解答 解：设等比数列{an}的首项为a1，由q=2，S8=6，得
$\frac{{a}_{1}（1-{2}^{8}）}{1-2}=6$，即${a}_{1}=\frac{6}{{2}^{8}-1}$．
∴a17+a18+a19+a20 =$\frac{{a}_{1}•{2}^{16}（1-{2}^{4}）}{1-2}$=$\frac{\frac{6}{{2}^{8}-1}•{2}^{16}（1-{2}^{4}）}{1-2}$=$\frac{3•{2}^{17}}{17}$．
故答案为：$\frac{3•{2}^{17}}{17}$．

点评 本题考查了等比数列的通项公式，考查了等比数列的性质，考查了等比数列的前n项和，是基础题．

练习册系列答案
相关题目
19．设两个非零向量$\overrightarrow a$与$\overrightarrow b$不共线，若$\overrightarrow{AB}=\overrightarrow a+\overrightarrow b，\overrightarrow{BC}=2\overrightarrow a+8\overrightarrow b，\overrightarrow{CD}$=$3（\overrightarrow a-\overrightarrow b）$，则（　　）
A．A，B，C三点共线B．B，C，D三点共线C．A，C，D三点共线D．A，B，D三点共线
20．求证：1+$\frac{1}{3^2}$+$\frac{1}{5^2}$+…+$\frac{1}{（2n-1）^2}$＞$\frac{7}{6}$-$\frac{1}{2（2n+1）}$．
17．极坐标中，椭圆C的中心在极点O，短轴端点为P（1，$\frac{π}{2}$），一个焦点为F（$\sqrt{3}$，0）．
（1）写出椭圆C的极坐标方程；
（2）点A、B在椭圆上，且OA⊥OB，求△AOB面积的最小值．
4．不等式${A}_{8}^{x}$＜6${A}_{8}^{x-2}$的解集为{8}．
14．化简：$\sqrt{2}$sin（$\frac{π}{4}$-x）+$\sqrt{6}$cos（$\frac{π}{4}$-x）
1．阅读如图所示的程序框图，若输入m=6，则输出S等于（　　）
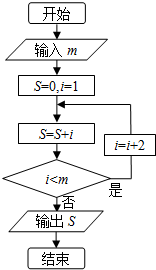
A．4B．9C．16D．25
18．不等式1＜|2x-1|＜3的解集为{x|-1＜x＜0或1＜x＜2}．
9．在校英语节演讲比赛中，七位评委老师为某班选手打出的分数的茎叶图（如图所示），去掉一个最高分和一个最低分后，所剩数据的方差为$\frac{8}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网