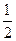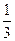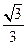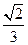题目内容
(本小题满分12分)
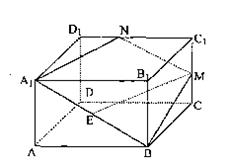
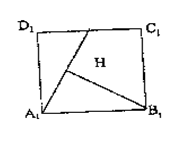
如图,在正四棱柱ABCD—A1B1C1D1中,AA1=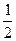 AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求二面角B—A1N—B1的正切值.

如图,在正四棱柱ABCD—A1B1C1D1中,AA1=
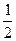 AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.(Ⅰ)求证:EM∥平面A1B1C1D1;
(Ⅱ)求二面角B—A1N—B1的正切值.
(Ⅱ)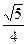
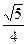
(Ⅰ)证明:取A1B1的中点F,连EF,C1F ∵E为A1B中点 ∴EF∥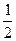 BB1 又∵M为CC1中点∴EF∥ C1M∴四边形EFC1M为平行四边形 ∴EM∥FC1
BB1 又∵M为CC1中点∴EF∥ C1M∴四边形EFC1M为平行四边形 ∴EM∥FC1
而EM 平面A1B1C1D1 . FC1
平面A1B1C1D1 . FC1 平面A1B1C1D1 .
平面A1B1C1D1 .
∴EM∥平面A1B1C1D1………………6分
(Ⅱ)由⑴EM∥平面A1B1C1D1
EM 平面A1BMN,平面A1BMN∩平面A1B1C1D1=A1N
平面A1BMN,平面A1BMN∩平面A1B1C1D1=A1N
∴A1N// EM// FC1 ∴N为C1D1中点,过B1作B1H⊥A1N于H,连BH,根据三垂线定理 BH⊥A1N
∠BHB1即为二面角B—A1N—B1的平面角……8分
设AA1=a,则AB=2a, ∵A1B1C1D1为正方形
∴A1H=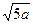 又∵△A1B1H∽△NA1D1
又∵△A1B1H∽△NA1D1
∴B1H=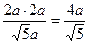 ,在Rt△BB1H中,
,在Rt△BB1H中,
tan∠BHB1=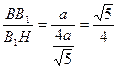 即二面角B—A1N—B1的正切值为
即二面角B—A1N—B1的正切值为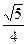 ……12分
……12分
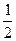 BB1 又∵M为CC1中点∴EF∥ C1M∴四边形EFC1M为平行四边形 ∴EM∥FC1
BB1 又∵M为CC1中点∴EF∥ C1M∴四边形EFC1M为平行四边形 ∴EM∥FC1 
而EM
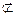 平面A1B1C1D1 . FC1
平面A1B1C1D1 . FC1 平面A1B1C1D1 .
平面A1B1C1D1 .∴EM∥平面A1B1C1D1………………6分
(Ⅱ)由⑴EM∥平面A1B1C1D1
EM
 平面A1BMN,平面A1BMN∩平面A1B1C1D1=A1N
平面A1BMN,平面A1BMN∩平面A1B1C1D1=A1N ∴A1N// EM// FC1 ∴N为C1D1中点,过B1作B1H⊥A1N于H,连BH,根据三垂线定理 BH⊥A1N
∠BHB1即为二面角B—A1N—B1的平面角……8分
设AA1=a,则AB=2a, ∵A1B1C1D1为正方形
∴A1H=
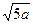 又∵△A1B1H∽△NA1D1
又∵△A1B1H∽△NA1D1∴B1H=
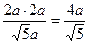 ,在Rt△BB1H中,
,在Rt△BB1H中,tan∠BHB1=
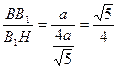 即二面角B—A1N—B1的正切值为
即二面角B—A1N—B1的正切值为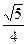 ……12分
……12分 
练习册系列答案
相关题目
 中,底面
中,底面 是平行四边形,
是平行四边形,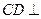 侧面
侧面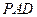 ,点在侧棱
,点在侧棱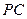 上,
上,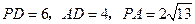 .
.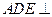 平面
平面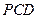 ;
;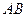 所成角为
所成角为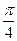 ,二面角
,二面角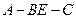 的大小为
的大小为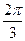 ,求
,求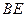 与平面
与平面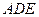 所成角的大小.
所成角的大小.
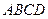 是
是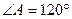 的菱形,绕AC将该菱形折成二面角
的菱形,绕AC将该菱形折成二面角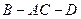 ,记异面直线
,记异面直线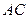 、
、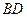 所成角为
所成角为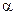 ,
,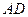 与平面
与平面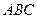 所成角为
所成角为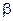 ,当
,当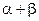 最大时,二面角
最大时,二面角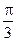
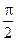
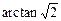
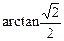
 分)如图,五面体
分)如图,五面体
 中
中
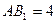 .底面
.底面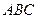 是正三角形,
是正三角形,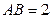 .
. 四边形
四边形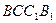 是矩形
是矩形 ,
, 二面角
二面角
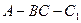 为直二面角.
为直二面角.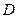 在
在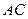 上运动,当
上运动,当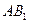 ∥平面
∥平面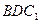 ,并且
,并且 说明理由;
说明理由;
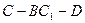
 的
的 余弦值.
余弦值.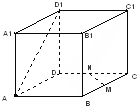
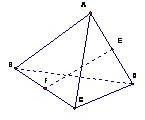
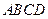 中,已知棱
中,已知棱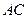 的长为
的长为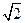 ,其余各棱长都为
,其余各棱长都为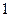 ,则二面角
,则二面角 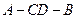 的余弦值为( )
的余弦值为( )