题目内容
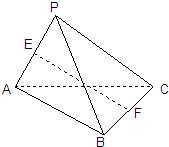
在三棱锥S-ABC中,若底面ABC是边长等于2
的正三角形,SA与底面ABC垂直,SA=6,点M,N分别为SB,AC的中点,则异面直线MN与BC所成角的大小为______.
| 3 |
取AB的中点D,连结MD,DN,因为M,N分别为SB,AC的中点,所以DN为三角形ABC的中位线,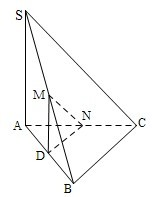
所以DN∥BC,且DN=
BC=
×2
=
,所以MN与DN所成的角即为异面直线MN与BC所成角,
因为SA与底面ABC垂直,所以DM∥SA,所以DM⊥ABC,
即DM⊥DN,所以三角形MDN为直角三角形.
因为DM=
SA=
×6=3,所以在直角三角形MDN中,
tanMDN=
=
=
,所以∠MDN=60°,
故异面直线MN与BC所成角的大小为60°
故答案为:60°

所以DN∥BC,且DN=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
因为SA与底面ABC垂直,所以DM∥SA,所以DM⊥ABC,
即DM⊥DN,所以三角形MDN为直角三角形.
因为DM=
| 1 |
| 2 |
| 1 |
| 2 |
tanMDN=
| DM |
| DN |
| 3 | ||
|
| 3 |
故异面直线MN与BC所成角的大小为60°
故答案为:60°

练习册系列答案
相关题目
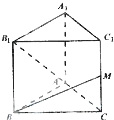
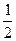 AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.
AB,点E、M分别为A1B、C1C的中点,过点A1,B,M三点的平面A1BMN交C1D1于点N.