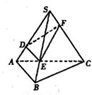
题目内容
一个半径为1的小球在一个内壁棱长为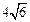 的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
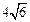 的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.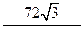
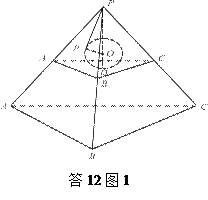
如答12图1,考虑小球挤在一个角时的情况,记小球半径为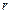 ,作平面
,作平面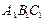 //平面
//平面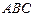 ,与小球相切于点
,与小球相切于点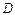 ,则小球球心
,则小球球心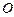 为正四面体
为正四面体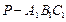 的中心,
的中心,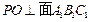 ,垂足
,垂足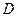 为
为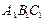 的中心.
的中心.

因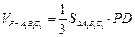

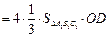 ,
,
故 ,从而
,从而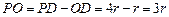 .
.
记此时小球与面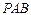 的切点为
的切点为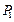 ,连接
,连接 ,则
,则
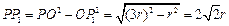 .
.
考虑小球与正四面体的一个面(不妨取为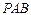 )相切时的情况,易知小球在面
)相切时的情况,易知小球在面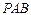 上最靠近边的切点的轨迹仍为正三角形,记为
上最靠近边的切点的轨迹仍为正三角形,记为 ,如答12图2.记正四面体
,如答12图2.记正四面体
的棱长为 ,过
,过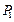 作
作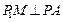 于
于 .
.
因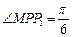 ,有
,有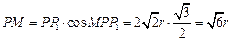 ,故小三角形的边长
,故小三角形的边长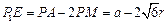 .
.
小球与面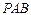 不能接触到的部分的面积为(如答12图2中阴影部分)
不能接触到的部分的面积为(如答12图2中阴影部分)
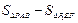

 .
.
又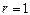 ,
,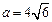 ,所以
,所以
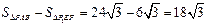 .
.
由对称性,且正四面体共4个面,所以小球不能接触到的容器内壁的面积共为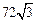 .
.
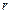 ,作平面
,作平面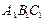 //平面
//平面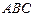 ,与小球相切于点
,与小球相切于点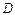 ,则小球球心
,则小球球心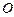 为正四面体
为正四面体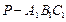 的中心,
的中心,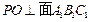 ,垂足
,垂足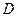 为
为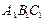 的中心.
的中心.

因
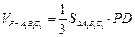

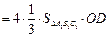 ,
,故
 ,从而
,从而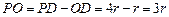 .
.记此时小球与面
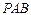 的切点为
的切点为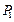 ,连接
,连接 ,则
,则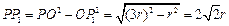 .
.考虑小球与正四面体的一个面(不妨取为
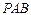 )相切时的情况,易知小球在面
)相切时的情况,易知小球在面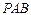 上最靠近边的切点的轨迹仍为正三角形,记为
上最靠近边的切点的轨迹仍为正三角形,记为 ,如答12图2.记正四面体
,如答12图2.记正四面体的棱长为
 ,过
,过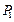 作
作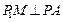 于
于 .
.因
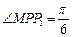 ,有
,有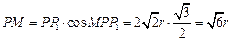 ,故小三角形的边长
,故小三角形的边长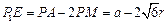 .
.小球与面
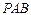 不能接触到的部分的面积为(如答12图2中阴影部分)
不能接触到的部分的面积为(如答12图2中阴影部分)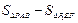

 .
. 又
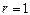 ,
,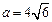 ,所以
,所以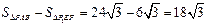 .
.由对称性,且正四面体共4个面,所以小球不能接触到的容器内壁的面积共为
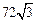 .
. 
练习册系列答案
相关题目
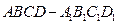 是一个棱长为1的正方体,
是一个棱长为1的正方体,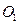 是底面
是底面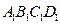 的中心,
的中心, 是棱
是棱 上的点,且
上的点,且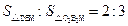 ,则四面体
,则四面体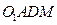 的体积为 ( )
的体积为 ( )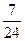
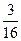
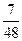
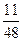
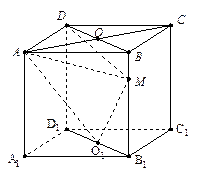
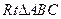 中,
中,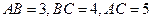 ,将三角形绕直角边
,将三角形绕直角边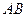 旋转一周所成
旋转一周所成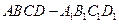 中,
中,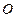 是上底面
是上底面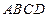 中心,若正方体的棱长为
中心,若正方体的棱长为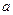 ,则三棱锥
,则三棱锥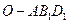 的体积为_____________。
的体积为_____________。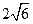 ,则侧面与底面所成的二面角等于_______________。
,则侧面与底面所成的二面角等于_______________。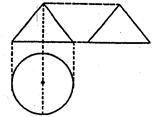
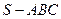 中,
中,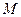 、
、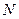 分别是棱
分别是棱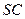 、
、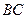 的中点,且
的中点,且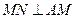 ,若侧棱
,若侧棱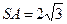 ,则正三棱锥
,则正三棱锥