题目内容
在球心同侧有相距9cm的两个平行截面,它们的面积分别为49πcm2和400π cm2,求球的表面积.
球的表面积为2 500π cm2
如图,为球的轴截面,?
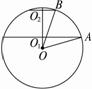
由球的截面性质知,AO1∥BO2,且O1、O2分别为两截面圆的圆心,?
则OO1⊥AO1,OO2⊥BO2.?
设球的半径为R.?
∵π·O2B2=49π,∴O2B=7(cm).?
同理πO1A2=400π,∴O1A=20(cm).?
设OO1=xcm,则OO2=(x+9)cm.?
在Rt△OO1A中,R2=x2+202,?
在Rt△OO2B中,R2=(x+9)2+72,?
∴x2+202=72+(x+9)2,
解得x=15.
∴R2=x2+202=252.
∴R=25(cm).
∴S球=4πR2="2" 500π(cm2).
∴球的表面积为2 500π cm2.

由球的截面性质知,AO1∥BO2,且O1、O2分别为两截面圆的圆心,?
则OO1⊥AO1,OO2⊥BO2.?
设球的半径为R.?
∵π·O2B2=49π,∴O2B=7(cm).?
同理πO1A2=400π,∴O1A=20(cm).?
设OO1=xcm,则OO2=(x+9)cm.?
在Rt△OO1A中,R2=x2+202,?
在Rt△OO2B中,R2=(x+9)2+72,?
∴x2+202=72+(x+9)2,
解得x=15.
∴R2=x2+202=252.
∴R=25(cm).
∴S球=4πR2="2" 500π(cm2).
∴球的表面积为2 500π cm2.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 倍
倍 倍
倍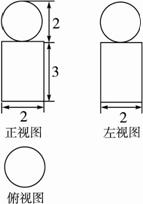

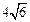 的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.
的正四面体容器内可向各个方向自由运动,则该小球永远不可能接触到的容器内壁的面积是.