题目内容
17.下列各组中的两个集合相等的是( )①P={x|x=2n,n∈Z},Q={x|x=2(n-1),n∈Z},②P={x|x=2n-1,n∈N+},Q={x|x=2n+1,x∈N+},③P={x|x2-x=0},Q={x|x=$\frac{1+(-1)^{n}}{2}$,n∈Z}.
| A. | ①②③ | B. | ①③ | C. | ②③ | D. | ①② |
分析 根据集合相等的定义,分别对①②③进行判断即可.
解答 解:对于①:P,Q都表示偶数,是相等集合;
对于②:P={1,3,5,7,••},Q={3,5,7,…},集合Q是集合P的子集,不相等;
对于③:P={0,1},Q={0,1},相等;
故选:B.
点评 本题考查了集合的相等问题,牢记定义是解题的关键,本题是一道基础题.

练习册系列答案
相关题目
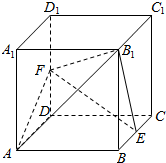 棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点.
棱长为1的正方体ABCD-A1B1C1D1中,E、F分别为棱BC、DD1的中点.