Question

【题目】已知两个定点 ，动点P满足 .设动点P的轨迹为曲线E，直线 .
（1）求曲线E的轨迹方程；
（2）若l与曲线E交于不同的C,D两点，且 （O为坐标原点），求直线l的斜率；
（3）若 是直线l上的动点，过Q作曲线E的两条切线QM,QN，切点为M,N，探究：直线MN是否过定点.

Answer 1

【答案】
（1）解：设点P坐标为
由 ，得：
整理得：曲线的E轨迹方程为 x 2 + y 2 = 4。
（2）解：依题意圆心到直线l的距离 ，
∴：k=±.
（3）解：由题意可知： 四点共圆且在以OQ为直径的圆上，设 ，
其方程为 ，即：
又M,N在曲线 上，
，
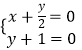即 ，由 得 ，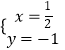
直线MN过定点 .
故答案为：直线MN过定点 ( , 1 ).
【解析】（1）本题先假设出点p的坐标，将已知条件代入即可求出轨迹方程。
（2）根据圆心到直线的距离可利用到未知数斜率k，进而求出k值。
（3）根据已知条件假设出以OQ为直径圆的方程，再假设出直线MN的方程式，进而代入即可求出直线MN是否过定点。