题目内容
【题目】如图，在三棱柱 
中，点E，F分别是棱CC1 ， BB1上的点，点M是线段AC上的动点，EC=2FB=2，若MB∥平面AEF，试判断点M的位置.
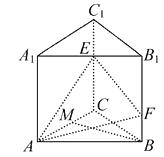
【答案】解：过F，B，M作平面FBMN交AE于N.
因为BF∥平面AA1C1C，BF 
平面FBMN，平面FBMN∩平面AA1C1C=MN，
所以BF∥MN.又MB∥平面AEF，MB 平面FBMN，平面FBMN∩平面AEF=FN，所以MB∥FN，所以BFNM是平行四边形，
所以MN=BF=1.又EC∥FB，EC=2FB=2，
所以MN∥EC，MN= 
，故MN是△ACE的中位线.
所以M是AC的中点时，MB∥平面AEF.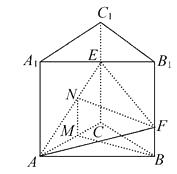
【解析】要使MB∥平面AEF，由过F，B，M作的平面FBMN与BF平行，再得到BFNM是平行四边形，故MN是△ACE的中位线.
练习册系列答案
相关题目
