题目内容
【题目】如图,直三棱柱ABC﹣A1B1C1中,AB=AC=AA1 , AB⊥AC,M是CC1的中点,N是BC的中点,点P在线段A1B1上运动. 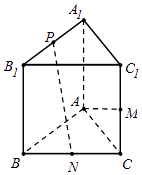
(Ⅰ)求证:PN⊥AM;
(Ⅱ)试确定点P的位置,使直线PN和平面ABC所成的角最大.
【答案】解:(Ⅰ)取AC的中点Q,连结A1Q,易知AM⊥A1Q,
又PN在平面A1C内的射影为A1Q,所以AM⊥PN.

(Ⅱ)作PD⊥AB于D,连结DN,则∠PND为直
线PN和平面ABC所成的角.易知当ND最短,即ND⊥AB
时, ![]() 最大,从而∠PND最大,此时D为AB的中点,P为A1B1的中点.
最大,从而∠PND最大,此时D为AB的中点,P为A1B1的中点.
【解析】(Ⅰ)取AC的中点Q,连结A1Q,易知AM⊥A1Q,可得AM⊥PN.(Ⅱ)作PD⊥AB于D,连结DN,则∠PND为直线PN和平面ABC所成的角.易知当ND最短,即ND⊥AB时,∠PND最大,此时D为AB的中点,P为A1B1的中点.

练习册系列答案
相关题目
