题目内容
16.已知向量$\vec a=(2sinθ,cosθ),\vec b=(\frac{1}{2},\frac{3}{2})$(Ⅰ)若$\vec a$∥$\vec b$,求tanθ的值;
(Ⅱ)若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,$θ∈(0,\frac{π}{2})$,求θ的值.
分析 (Ⅰ)利用$\vec a$∥$\vec b$,列出方程,即可求tanθ的值;
(Ⅱ)利用|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,$θ∈(0,\frac{π}{2})$,得到余弦函数值,然后求θ的值.
解答 本小题满分(10分).
解:(Ⅰ) 因为$\vec a$∥$\vec b$,所以$\frac{1}{2}cosθ=3sinθ$------------------------------------(2分)
故$tanθ=\frac{1}{6}$------------------------------------(4分)
(Ⅱ)由|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,知,$4{sin^2}θ+{cos^2}θ=\frac{1}{4}+\frac{9}{4}=\frac{5}{2}$-----------------------------------(6分)
即$4-4{cos^2}θ+{cos^2}θ=\frac{5}{2}⇒3{cos^2}θ=\frac{3}{2}⇒{cos^2}θ=\frac{1}{2}$,------------------(8分)
即$cosθ=±\frac{{\sqrt{2}}}{2}$,------------------------------------(9分)
又由$θ∈(0,\frac{π}{2})$得到 $θ=\frac{π}{4}$------------------------------------(10分)
点评 本题考查向量的共线以及向量的模的求法,三角函数的化简求值考查计算能力.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
6.已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1,2cosC+c=2b,则△ABC的周长的取值范围是( )
| A. | ($\frac{1}{2},2$] | B. | (1,3] | C. | (2,3] | D. | [3,5] |
8.有5道题中,有3道理科题和2道文科题,如果不放回地依次抽取2道题,则在第1次抽到理科题的条件下,第2次抽到理科题的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
5.给出如下“三段论”推理:
因为整数是自然数,…大前提
而-5是整数,…小前提
所以-5是自然数.…结 论
则( )
因为整数是自然数,…大前提
而-5是整数,…小前提
所以-5是自然数.…结 论
则( )
| A. | 这个推理的形式错误 | B. | 这个推理的大前提错误 | ||
| C. | 这个推理的小前提错误 | D. | 这个推理正确 |
6.某四面体的三视图如图所示,该四面体四个面的面积中最大的是( )
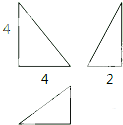

| A. | 8 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{5}$ | D. | 10 |