题目内容
1.已知x,y为正实数,若关于x,y的不等式$\frac{3x}{2x+y}$+$\frac{3y}{x+2y}$≤m2+m恒成立,则实数m的取值范围是(-∞,-2]∪[1,+∞).分析 设2x+y=m,2y+x=n 且m,n均为正数则3x=2m-n,3y=2n-m,$\frac{3x}{2x+y}$+$\frac{3y}{x+2y}$转化为$\frac{2m-n}{m}$+$\frac{2n-m}{n}$=2+2-$\frac{n}{m}$-$\frac{m}{n}$,利用基本不等式即可求出最大值,由题意得到m2+m≥2,解得即可.
解答 解:设2x+y=m,2y+x=n 且m,n均为正数
则3x=2m-n,3y=2n-m,
所以$\frac{3x}{2x+y}$+$\frac{3y}{x+2y}$=$\frac{2m-n}{m}$+$\frac{2n-m}{n}$=2+2-$\frac{n}{m}$-$\frac{m}{n}$≤4-2$\sqrt{\frac{m}{n}•\frac{n}{m}}$=2,当且仅当m=n时取等号,
∵关于x,y的不等式$\frac{3x}{2x+y}$+$\frac{3y}{x+2y}$≤m2+m恒成立,
∴m2+m≥2,
解得m≤-2,或m≥1,
故实数m的取值范围是(-∞,-2]∪[1,+∞),
故答案为:(-∞,-2]∪[1,+∞).
点评 本题考查了恒成立的问题,关键是利用基本不等式求出$\frac{3x}{2x+y}$+$\frac{3y}{x+2y}$的最大值,属于中档题.

练习册系列答案
相关题目
11.设{an}是等差数列,{bn}是等比数列,且a1=b1,a2015=b2015,则( )
| A. | a1008>b1008 | B. | a1008≥b1008 | ||
| C. | a1008<b1008 | D. | 以上答案均有可能 |
12.(2-x)10=a0+a1x+a2x2+…+a10x10.则a1+a2+a3+…+a10=( )
| A. | 1 | B. | -1 | C. | 1023 | D. | -1023 |
9.在四边形ABCD中,若$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,且$|{\overrightarrow{AB}}|=|{\overrightarrow{AD}}|$,则( )
| A. | ABCD是矩形 | B. | ABCD是菱形 | ||
| C. | ABCD是正方形 | D. | ABCD是平行四边形 |
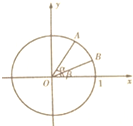 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为$\frac{5}{13},\frac{3}{5}$,则tan(α+β)的值为-$\frac{56}{33}$.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A、B两点,已知A、B的横坐标分别为$\frac{5}{13},\frac{3}{5}$,则tan(α+β)的值为-$\frac{56}{33}$.